- Axelrod, R. (2016). 合作的进化 (吴坚忠, 译). 上海人民出版社.
什么条件下才能从没有集权的利己主义者中产生合作? 本书在重复囚徒困境博弈的假设下, 用中学生都能懂的数学和模型推断出整个系统的行为结果. “一报还一报” 在该设定下是稳健策略, 它的收益总是不高于博弈的对手, 但能通过促成合作 (不需要参与者利他主义), 在作者组织的算法竞赛中得到最高的收益.
“没有集权的利己主义者” 这个假设的局限性很小. 本书提出的合作理论基于追求自身利益的个体. 这些个体中没有中心权威强迫他们合作, 彼此的合作不是完全基于关心他人或者考虑群体利益.
定性小结
合作理论的主要结论令人鼓舞, 它说明即使在一个其他人不愿意合作的世界, 仍然可以通过一小群愿意回报合作的人产生合作. 合作能发展的两个关键前提是合作要基于回报, 以及未来的影响要足够重要使得回报稳定. 基于回报的合作一旦在群体中建立, 它就能使自己免受非合作策略的侵入.
“一报还一报” 策略的成功是由于它友善 (nice), 敢怒 (provocable), 宽容 (forgiving), 清晰 (clean). 友善意味着绝不首先背叛, 防止它陷入不必要的麻烦. 敢怒使得对方尝试背叛后不敢再犯. 宽容有助恢复互相合作. 清晰使它的行为方式容易辨识, 并且容易看出与它想出的最好方式就是互相合作.
这些结果绘出了一幅合作进化的图景. 合作能从小群体开始, 在友善, 敢怒, 一定限度的宽容的规则中逐步成长. 一旦成为一个群体, 采用这种易于辨识的策略的个体就不会被侵入. 总体的合作水平总是上升, 即合作的进化是不可逆的.
合作进化所必要的不是友谊, 而是关系持续 (即便是敌对关系). “一报还一报” 的成功不是由于它比它打交道的任何人做得更好. 它的成功是靠从其他人那里引出合作而不是靠背叛他们. 我们习惯于把竞争考虑成只有一个胜利者, 像踢足球或下棋; 但世界上的事情很少像这样. 在很多情况下, 双方合作比双方背叛好. 做得好的关键不在于征服对方而在于引导合作.
对参与者
- 不要嫉妒 (对方收益更高). 这不是零和游戏.
- 不要首先背叛.
- 对合作与背叛都给予回应.
- 不要耍小聪明. 非零和博弈不像预测天气, 对方对你的行为有反应; 也不像下棋的对手, 对方不应该被认为是一心想背叛你的. 对方将你的行为看作你是否回报合作的信号. 因此你的行为会反应到自己身上.
如何促进合作
- 增大未来的影响
- 改变收益值. 比如政府执行的法律.
- 教育人们互相关心 (他人的利益).
- 教育人们要回报.
- 改进辨别能力.
证明
囚徒困境中, 个体对自身利益的追求将损害整体的利益.
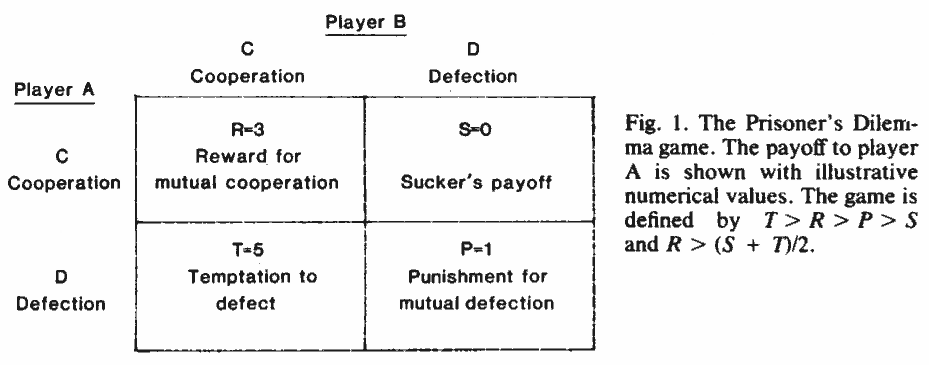
囚徒困境的博弈矩阵如上 (博弈论基础略), 需满足两个条件
- $T > R > P > S$.
- $2R > T + S$, 即不能通过交替的背叛合作 (A 背叛 B 合作, 下一轮 A 合作 B 背叛) 达到比双方一直合作更好的效果.
进一步说明 (Show more »)
- 参与者的收益不必可比较 (可以是完全不同的东西).
- 收益不必对称. 只需要对每个参与者来说, 四种收益符合上述条件.
- 不必假设参与者是理性的. 不必假设他们总是力争最大收益, 他们的行为不必都是有意识的选择.
于是这个框架之大, 不仅包含了人, 而且大到国家 (比如关税升降) 小到细菌 (对周围化学环境和有机体做出反应) 均包含在内.
最优选择是互相背叛 (Nash 均衡). 若重复有限次囚徒困境, 则由于最后一次一定背叛, 可得倒数第二次也背叛, 从而每次都背叛. 然而 无限次 进行博弈时情况有所不同 (好像有些偷换概念, 前面有限次没有衰减系数, 而无限次必须有衰减系数).
重复 (iterated) 囚徒困境是指双方无限次进行囚徒困境博弈, 合作可能出现是因为双方会再次相遇. 第二次的收益 (payoff) 相比第一次要乘上一个 折扣系数 (discount parameter) $w \in (0, 1)$, 以此类推 (系数不变). 这个折扣类似于现金折现——同面值的金额现在得到比未来得到更有价值, 也可以理解为下一次遇到对方进行博弈的概率 (去世, 迁移到别地等).
一个典型的策略是 “一报还一报” (tit for tat), 即第一步选择合作, 之后重复对手上一次的选择 (若对手第一次选背叛, 则我方第二次也选背叛; 合作则继续合作).
如果未来足够重要, 则重复囚徒困境不存在最佳策略.
命题 1. 如果折扣系数 $w$ 足够大, 则不存在独立于其他人所采用策略的最优策略.
证明 假设对方使用 “总是背叛” 策略, 显然我方最优策略亦为总是背叛. 另外, 假设对方采用 “永久报复” 的策略, 即首先采取合作直到你背叛, 然后就一直背叛.
- 若我方一直背叛, 收益为 $v_1 = T + \sum_{k=1}^\infty w^k P = T + wP / (1-w)$.
- 若我方一直合作, 收益为 $v_2 = \sum_{k=0}^\infty w^k R = R / (1-w)$.
若 $v_1 < v_2$, 即 $w > (T-R)/(T-P)$ 时, 则总是背叛不再是我方最优策略. $\square$
假设一个群体中所有个体都采用相同策略, 另外有一个变异个体采用不同策略, 他是否有理由这么做. 若变异个体与前述群体任意个体博弈的收益比其他人高, 则称该变异策略可以 侵入 (invade) 这个群体, 意味着其他人改用变异策略可以获得更高收益. 若一个策略不能被其他策略侵入, 则称这个策略是 集体稳定的 (collectively stable).
如果所有人都一报还一报, 且未来足够重要, 则没人能通过改变策略而做到更好.
命题 2. “一报还一报” 策略集体稳定的充要条件是
\[w \ge \max\left\{ \frac{T-R}{T-P}, \frac{T-R}{R-S} \right\}.\]证明 关键在于 “一报还一报” 策略只有上一步的记忆, 以及折扣系数 $w < 1$.
- 如果对抗一报还一报的最优策略的第一步选 C (合作). 则由于一报还一报第二步还是 C, 情况与第一步相同, 再考虑到折扣系数, 最优对抗策略的第二步必然和第一步相同, 从而选择一直合作, 而这与一报还一报内战相同.
- 如果最优对抗策略第一步选 D (背叛). 如果第二步选 C, 则第三步变成与第一步相同的情况, 从而最优对抗策略为重复 DC (交替背叛合作); 如果第二步选 D, 则第三步变成与第二步相同的情况, 从而最优对抗策略为重复 DD (总是背叛).
如果这两个策略不能侵入一报还一报策略, 则后者就是集体稳定的.
考虑总是背叛, 证明同命题一, 可知 $w \ge (T-R)/(T-P)$ 时, 不能侵入一报还一报. “交替背叛合作” 策略对上一报还一报的收益为
\[\sum_{k=0}^\infty w^{2k}(T + wS) = (T + wS) / (1-w^2),\]故当 $w \ge (T-R) / (R-S)$ 时, 不能侵入一报还一报. $\square$
记 $V(A\mid B)$ 为策略 A 与策略 B 博弈时, 策略 A 的收益. 记 $V_n(A \mid B)$ 为前述博弈第 $n$ 步前 (不包括) A 的收益. 面对单体入侵者, 群体中任意一个个体的收益只考虑内战的收益, 忽略和侵略者博弈收益.
下面给出所有集体稳定策略的刻画. 如果策略 B 可以不管策略 A 怎么做都能使 A 的收益足够低, B 就不会被 A 侵入. This leads to the following useful definition: B has a secure position over A on move $n$ if no matter what A does from move $n$ onward, $V(A \mid B) \le V(B \mid B)$, assuming that B defects from move $n$ onward. 即
\[V_n(A \mid B) + w^{n-1}P / (1-w) \le V(B \mid B).\]The theorem which follows embodies the advice that if you want to employ a collectively stable strategy, you should only cooperate when you can afford an exploitation by the other side and still retain your secure position. (这句话中译版是错的.)
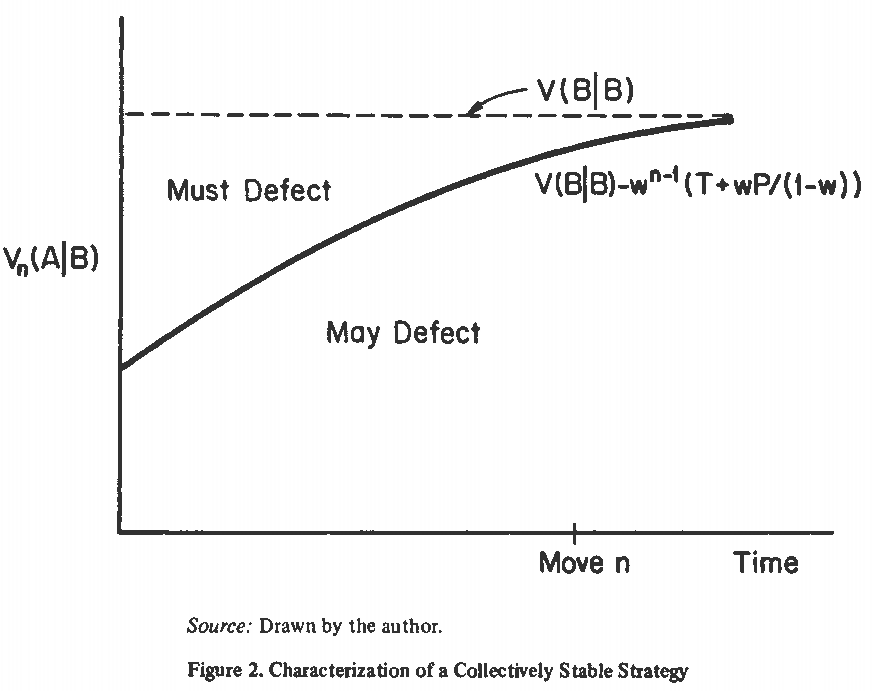
刻画定理. 策略 B 集体稳定的充要条件是, 在对方累积收益足够大的第 $n$ 步选择背叛, 即使得
\[V_n(A \mid B) + w^{n-1}\left[ T+ wP/(1-w) \right] > V(B \mid B)\]的 $n$.
证明 改编自 Axelrod, R. (1981). The emergence of cooperation among egoists. American political science review, 75(2), 306-318.
必要性显然 (反证), 下证充分性 (也显然), 对任意 A, 策略 B 如上背叛时, 每步都相对 A 具有安全地位, 因此 B 集体稳定. 对于第一步, 由安全地位的定义,
\[0 + P/(1-w) \le V(B \mid B)\]显然成立 (原证明写的好像有问题). 下面递归证明, 如果 B 在第 $n$ 步相对 A 具有安全地位, 则在第 $n+1$ 步也有.
首先, 如果 B 在第 $n$ 步背叛, 则
\[V_{n+1}(A \mid B) \le V_n(A \mid B) + w^{n-1} P.\]再由安全地位的定义递推可得第 $n+1$ 步也具有安全地位.
其次, 如果 B 在第 $n$ 步合作, 由定理条件, 以及第 $n$ 步 A 最多得到 $w^{n-1}T$, 由安全地位的定义可得第 $n+1$ 步也具有安全地位. $\square$
命题 3. 任何可能首先合作的策略 B, 只有在 $w$ 足够大时, 才可能是集体稳定的.
证明 如果 B 在第一步合作, 那么
\[V(\text{ALL D} \mid B) \ge T + wP/(1-w) := v_1,\]其中 ALL D 表示一直背叛. 因为囚徒困境的假设, $R > \max\{ P, (S+T)/2 \}$, 因此对任何 B,
\[V(B \mid B) \le R/(1-w) := v_2.\]若 $v_1 > v_2$, 即 $w < (T-R) / (T-P)$ 时, $V(\text{ALL D} \mid B) > V(B \mid B)$, 此时 “总是背叛” 策略可以侵入第一步合作的策略 B. (原文感觉有点问题, 下面转述) 因此只有 $w$ 足够大, B 才有可能不被 “总是背叛” 侵入. 如果 B 在第 $n$ 步前不会首先合作, 则 $V_n(\text{ALL D} \mid B) = V_n(B \mid B)$, 之后情况同上. $\square$
友善的 (nice) 策略指绝不首先背叛的策略.
命题 4. 一个友善策略集体稳定的必要条件是, 它能被对方的第一个背叛激怒.
证明 如果一个友善的策略没有被第 $n$ 步的背叛激怒 (即之后选择背叛), 则它会被只在第 $n$ 步背叛的策略侵入, 因此不是集体稳定的. $\square$
命题 5. “总是背叛” 策略是集体稳定的.
显然.
也就是说一个 “小人” 的世界能阻止任何采用其他策略的单体侵入. 但如果新来者是一个小群体, 情况有所不同. 假设新来者 A 相对于已经建立起群体的 B 数量少到忽略不计. By clustering together the A’s can provide a significant part of each other’s environment, but a negligible part of the B’s environment. 若存在 $0 < p < 1$, 使得
\[p V(A \mid A) + (1-p) V(A \mid B) > V(B \mid B),\](原文有误) 则称 A 的 $p$-cluster 侵入 B, 其中 $p$ 是策略 A 内战的概率 (相遇概率非均匀分布, 会偏大), 忽略 B 与 A 对局的概率 (A 数量很小, 对于 B 来说可以忽略). 若 A 人数更多, 占 A 和 B 总人口的比例为 $q$, 则随机相遇时 (均匀分布),
\[q V(A \mid A) + (1-q) V (A \mid B) > q V(B \mid A) + (1-q) V(B \mid B),\]则 A 可侵入 B.
举个例子, $T =5$, $R=3$, $P=1$, $S=0$, $w=0.9$, 则当 $p > 1/20$ 或 $q > 1/17$, “一报还一报” 可以侵入 “总是背叛”.
下一结果说明能以最小的群体侵入 “总是背叛” 的策略是最能把它们自己和 “总是背叛” 区分开来的策略. Maximally discriminating 策略定义为, 若一个策略在即使对方从不合作的情况下最终也会合作, 并且一旦合作, 它不会再和 “总是背叛” 合作, 而总是和用相同策略的人合作.
命题 6. 能以最小的 $p$ 值侵入 “总是背叛” 的策略是 maximally discriminating 策略, 比如 “一报还一报”.
证明 一个策略要侵入 “总是背叛”, 必须有正的概率首先选择合作. 因为囚徒困境假设 $2R > T+S$, 因此和另一个相同规则随机选择合作不如确定的一直合作. 因此即使对方一直没有合作, 也要在某个第 $n$ 步首先选择合作. 由定义可知最小的 $p$ 为
\[p^\ast = \frac{V(B \mid B) - V(A \mid B)}{V(A \mid A) - V(A \mid B)},\]其中 A 为入侵群体的策略, B 为 “总是背叛”. 因为 $V(A \mid A) > V(B \mid B) > V(A \mid B)$, 当 $V(A \mid A)$ 和 $V(A \mid B)$ 最大时 (满足 A 在第 $n$ 步首先合作的约束), $p^\ast$ 最小. 而达到前述最大值的充要条件是 A 是 maximally discriminating 策略. “一报还一报” 就是这样的策略, 它在第 $n=1$ 步时合作, 它和 “总是背叛” 只合作一次, 而内战时永远合作. $\square$
命题 7. 如果一个友善的策略不能被单一个体侵入, 它也不会被这种策略的任何小群体侵入.
证明 记入侵者为 A, 友善策略为 B, 因为 $V(A \mid A) \le V(B \mid B)$ (由假设 $2R > T + S$). 因此由 $p$-cluster 入侵的定义, 只有当 $V(A \mid B) > V(B \mid B)$ 时, 才有可能侵入, 而这等价于单体侵入. $\square$
最后讨论只和邻居博弈的领地系统. 每一代, 每个参与者的收益为它与邻居博弈的平均值. 下一代, 参与者改用上一代收益最高的邻居所用的策略 (最高收益相同时随机选择). 如果采用策略 A 的个体引入到采用策略 B 的群体中, 且按照上述方式这个领地中所有参与者最终都转变到策略 A, 则称 A 领地侵入 (territorially invade) B. 如果没有策略能领地侵入 B, 则策略 B 为领地稳定的 (territorially stable).
命题 8. 如果一个策略是集体稳定的, 则它也是领地稳定的.
中译版的问题
翻译和排版太菜.
排版 数学变量没有用斜体 (根本没有数学模式的意识); 括号用了半角, 与全角引号产生显眼的丑陋间距, 也导致标点和字之间的空格不一致.
翻译 虽然译者懂博弈论, 但翻译只会字字一一对应, 一点也不懂翻译 (建议可以当翻译反面教材). 翻译菜一点可以理解, 但是错译就很离谱了. 比如 p52 S 写成了 5, 附录 B 刻画定理错翻为特化性定理, 另外附录 B 也是 typo 和错译的集中地, 以及隔了两行的前后术语不一致等 (其他章节我看得没有附录仔细), 不一一指出.