狮子与基督徒问题 一头狮子和一个基督徒在古罗马圆形竞技场中以相同的最大速度移动. 狮子能在有限时间内抓到基督徒吗? (为什么牵扯到基督徒可以参考 这里.)
上个世纪 30 年代德裔英国数学家 Richard Rado 提出了上述问题, 称为狮子与人问题 (Lion and Man problem). 把这个问题当做数学问题, 作以下假设:
- 不考虑体力等现实因素
- 狮子和基督徒各为一个点 (没有体积)
- 竞技场为闭圆盘 (后面会改变这个假设)
本文来自
- Schleicher, D., & Lackmann, M. (Eds.). (2011). An invitation to mathematics: From competitions to research. Springer Science & Business Media.
一书中由 Bollobás 撰写的 The Lion and the Christian, and Other Pursuit and Evasion Games 一章. 有趣的问题, 简单的数学. 更详细的讨论需要参考他的论文
- Bollobás, B., Leader, I., & Walters, M. (2009). Lion and Man–Can Both Win?. arXiv preprint arXiv:0909.2524.
解答
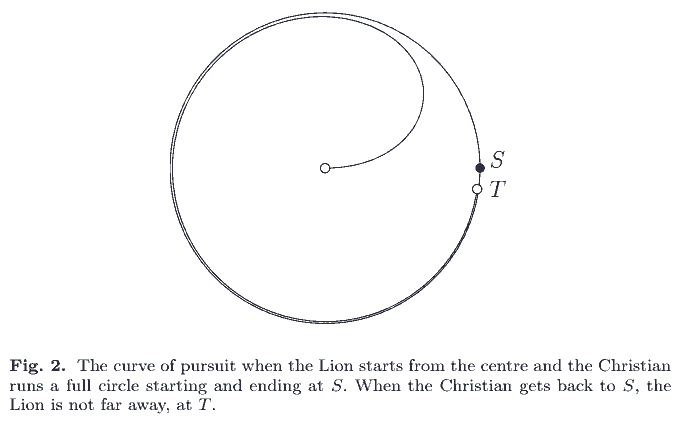
解答: 追踪曲线. 显然狮子的最佳策略是径直跑向基督徒, 那么基督徒就应该沿着闭圆盘边界全速奔跑. 于是狮子的运动轨迹形成了追踪曲线 (curve of pursuit), 它会无限接近基督徒, 但永远抓不到.
结论. 基督徒获胜.
上述狮子的 “最佳策略” 并不对. 在给出另一种解答前先引入一些记号. 记 $B$ 为野兽 (beast) 的位置, $C$ 为基督徒 (Christian) 的位置. 记 $D$ 为以 $O$ 为圆心的单位闭圆盘, 双方最大速度为 1.
解答二: 沿小圆移动. 狮子保持位于线段 $OC$ 上全速奔向基督徒. 如果基督徒依然沿着闭圆盘边界跑会如何? 简单起见, 假设基督徒 $C$ 以边界上的 $S$ 点为起点逆时针跑动; 狮子 $B$ 以圆心 $O$ 为起点.
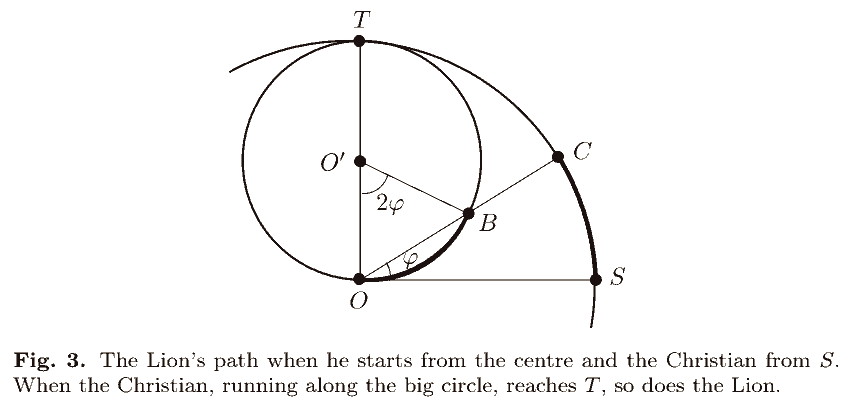
结果基督徒的轨迹为从 $S$ 到 $T$ 的四分之一圆, 狮子轨迹为从 $O$ 到 $T$ 的小半圆 ($B$ 始终在线段 $OC$ 上), 在 $T$ 点抓到基督徒. 显然不论基督徒如何变向都难逃一死.
结论. 狮子获胜.
这个解答保持了约二十年. 它很漂亮但很无聊: 数学家们不屑一顾. 直到 20 世纪 50 年代的一道晴天霹雳, 俄裔英国数学家 Abram S. Besicovitch 发现了下述巧妙解答.
解答三: 沿无限长的分段路径移动. 不妨设基督徒的起始位置 $C_1 \ne O$, 狮子的起始位置 $B_1 \ne C_1$. 记 $r_1$ 为线段 $OC_1$ 的长度 $\overline{OC}_1$, 其中 $0<r_1<1$.
把 (无限的) 时间分割为一系列时间段 $t_1, t_2, …$, 使得 $\sum_{i=0}^\infty t_i^2 < 1$, 其中 $t_0=r_1$. 因为 $\sum_{k=1}^\infty (1/k) = \infty$ 而且 $\sum_{k=1}^\infty (1/k^2)$ 有限, 比如可以取 $t_k = 1/(k+c)$, 其中 $c$ 足够大.
记时刻 $s_i = \sum_{j=0}^{i-1} t_j$, 时刻 $s_i$ 到 $s_{i+1}$ 的时间段称为第 $i$ 步. 假设在时刻 $s_i$, 基督徒位于 $C_i \ne O$, 狮子在 $B_i \ne C_i$, 并且 $r_i = \overline{OC} _i$, 其中 $r_i^2 = \sum _{j=0}^{i-1} t_j^2 < 1$.
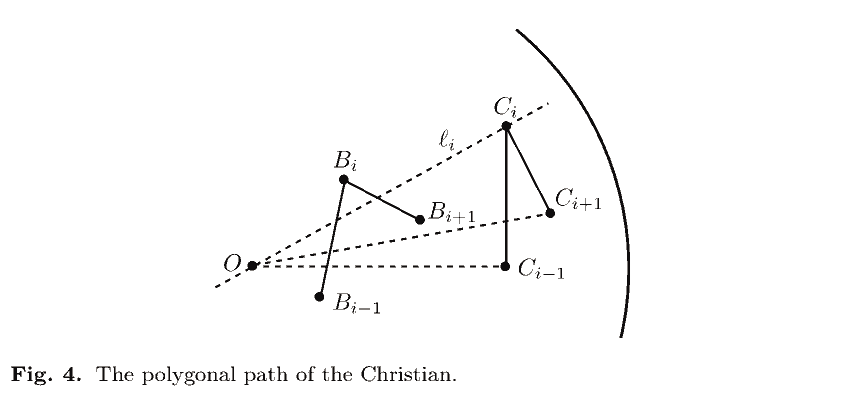
在第 $i$ 步, 基督徒沿着远离狮子位置 $B_i$ 并且垂直于 $OC_i$ 的方向以速度 1 跑动 $t_i$ 时间. 记 $l_i$ 为经过 $O$ 和 $C_i$ 的直线. 直线 $l_i$ 将圆分为两个半圆, 远离狮子意为着跑向狮子不在的另一个半圆. 因为狮子一定在另一个半圆或者在直线 $l_i$ 上, 所以它一定不能在第 $i$ 步抓到基督徒.
在 $s_{i+1}$ 时刻, 由勾股定理,
\[\overline{OC}_{i+1}^2 = r_i^2 + t_i^2 = \sum_{j=0}^i t_j^2 < 1.\]因此基督徒跑动的路径 $C_1 C_2…$ 长度无限, 并且不会跑出单位圆盘.
结论. 基督徒获胜.
这个解答同时说明了斗技场的形状不重要.
数学形式化
问题来了, 如何定义 “必胜策略”? 如果双方交替行动, 那么没有问题: 必胜策略指不论对手做什么都能取胜的策略. 但在连续时间就不一样了.
记狮子起始位置为 $x_0$, 基督徒 $y_0$, 最大速度为 1. 狮子的移动路径为映射 $f\colon [0, \infty) \to D$, 其中 $f(0) = x_0$, 并且满足 Lipschitz 条件 $\vert f(t) - f(t’) \vert \le \vert t - t’ \vert$ (因为最大速度为 1), 狮子在时刻 $t$ 的位置为 $f(t)$. 类似地, 基督徒的路径定义为 $g(t)$.
记 $\mathcal B$ 为狮子路径的集合 (映射的集合), $\mathcal C$ 为基督徒路径的集合. 基督徒的一个策略即映射 $\Phi\colon \mathcal B \to \mathcal C$, 使得如果 $f_1, f_2\in\mathcal B$ 直到时刻 $t_0$ 相等 (即 $f_1(t) = f_2(t)$ 对任意 $t\in [0, t_0]$ 成立), 则 $\Phi(f_1)$ 与 $\Phi(f_2)$ 也在 $[0, t_0]$ 上相等. 这个 “不能预知未来” 的限制意为着 $\Phi(f)(t)$ 只依赖于 $f$ 在区间 $[0, t]$ 上的限制. 狮子的策略 $\Psi$ 也类似定义. 若对任意 $f\in\mathcal B$, 以及任意 $t>0$, 都成立 $\Phi(f)(t) \ne f(t)$, 则称基督徒的策略 $\Phi$ 为必胜 (winning). 类似地定义狮子的必胜策略.
我们已经知道了基督徒有必胜策略;
但狮子会不会也有必胜策略?
怎么可能双方都有必胜策略? 如果双方同时用必胜策略, 那最终双方都取胜, 显然矛盾.
但上一句的 “论证” 是错的. 如何让双方同时执行必胜策略? 假设双方同时执行必胜策略时, 狮子和基督徒分别用策略 $\Phi$ 和 $\Psi$, 狮子路径 $f$, 基督徒路径 $g$. 其中 $\Phi(f) = g$ 并且 $\Psi(g) = f$; 特别地, $\Psi(\Phi(f)) = f$, 即 $f$ 是复合映射 $\Psi \circ \Phi\colon \mathcal B \to \mathcal B$ 的不动点. But why should the composite map have a fixed point at all? There is no reason why it should.
因此, 在一般的追及 (pursuit–evasion) 问题中, 有两个基本问题. (1) 狮子是否有必胜策略? (2) 基督徒是否有必胜策略? 这两个问题答案的四种组合都会出现吗? 这个问题的回答见 Bollobás (2009).
如果双方轮流行动, 那么可以根据对方的策略执行自己的策略, 此时双方不可能同时有必胜策略. 连续时间博弈的问题是双方可以即时对对手策略进行反应.
还有一些自然的问题, 比如说是否存在 “合理 (nice)” 的必胜策略? 最显然的定义 “合理” 的方式是连续性 ($\Phi$ 和 $\Psi$ 连续). 策略 $\Phi\colon \mathcal B\to \mathcal C$ 是连续的, 若对任意 $f_0\in\mathcal B$, 任意 $\varepsilon>0$, 存在 $\delta>0$, 使得对任意 $f_1 \in \{f\in\mathcal B : \vert f_0(t) - f(t) \vert <\delta \text{ for any } t \}$, 都成立 $\vert \Phi(f_0)(t) - \Phi(f_1)(t) \vert < \varepsilon$ for any $t$.
结果
可以证明狮子没有必胜策略. 上文策略三是基督徒的必胜策略, 但是这个策略连续吗? 考虑 $O$, $B$, $C$ 共线的情况, 可知这个策略不连续. 事实上
原问题双方都没有连续的必胜策略. 令狮子从原点出发, 对基督徒的任意连续策略, 存在于时刻 1 抓住基督徒的狮子路径.
证明. 令 $\Phi\colon \mathcal B \to \mathcal C$ 为基督徒的连续策略. 对任意 $z\in D$, 令 $h_z(t) = tz$, 即从原点开始以速度 $z$ 匀速直线运动. 显然 $z\mapsto h_z$ 是 $D$ 到 $\mathcal B$ 的连续映射, 从而 $z\mapsto \Phi(h_z)(1)$ 是 $D$ 到 $D$ 的连续映射. 由 Brouwer 不动点定理 (紧凸集上的任意连续映射有不动点), 上述映射存在不动点 $z_0\in D$, 即 $\Phi(h_{z_0})(1) = z_0$. 因此如果狮子按照 $h_{z_0}$ 移动, 基督徒执行策略 $\Phi$, 则狮子可以在时刻 1 抓到基督徒. $\square$
下面的问题相当 tricky.
在紧度量空间 (取代之前的单位闭圆盘) 上展开博弈.
双方都有必胜策略的博弈. 令博弈场地为闭的实心圆柱
\[D\times I = \{ (a,z): a\in D, z\in [0,1] \}.\]对其中任意两点 $(a,z), (b, u) \in D\times I$, 距离定义为
\[\max\{|a-b|, |z-u| \}.\]起始位置, $C$ 在圆柱顶部中心, $B$ 在底部中心. 则双方都有必胜策略.
证明. 狮子的必胜策略很简单. 保持圆盘的坐标 (第一个维度 $D$) 和人相同, 同时在纵轴 (第二个维度 $I$) 以速度 1 往上移动. 经过 1 单位时间后可以抓到人. 这里狮子利用了此空间的距离是 $\ell_\infty$ 距离, 而非通常的欧氏距离.
人的必胜策略在于设法在 1 单位时间内使人的圆盘坐标和狮子的不同 (使人不在狮子正上方), 之后用上文策略三即可. $\square$
上述双方策略不能同时执行 (cannot be played against each other).

(我没懂人这样怎么和狮子偏移开)
开区间上的博弈. 在开区间 $(0, 1)$ 上, 基督徒起始在 1/3 狮子起始在 2/3, 则双方都有必胜策略.
基督徒的必胜策略为
\[f(t) \mapsto f(t)/2.\]回忆 $f(t)$ 表示狮子路径, $g(t)$ 表示基督徒路径. 上述策略说基督徒保持位置是狮子的 1/2.
狮子的必胜策略为
\[g(t) \mapsto \max\{ 2/3 -t, g(t) \}.\]即向左以速度 1 匀速运动. 所以 2/3 时间内一定遇到人.
(还是好怪)