算法分析的那个定理.
Master Theorem
\[T(n) = \begin{cases} \Theta(1), & \text{if } n = 1,\\ aT(n/b) + f(n), & \text{if } n>1. \end{cases}\]where $a\ge1$, $b>1$ are constants and $f$ is nonnegative. Then
- If $f(n) = O(n^{\log_b a-\varepsilon})$ for some constant $\varepsilon >0$, then $T(n) = \Theta(n^{\log_b a})$.
- If $f(n) = \Theta(n^{\log_b a})$, then $T(n) = \Theta(n^{\log_b a}\log n)$.
- If $f(n) = \Omega(n^{\log_b a+\varepsilon})$ for some constant $\varepsilon >0$, and if $af(n/b)\le cf(n)$ for some constant $c<1$ and all sufficiently large $n$, then $T(n) = \Theta(f(n))$.
直观上看就是比较 $f(n)$ 与 $n^{\log_b a}$ 的阶数, 其中大的决定了 $T(n)$ 的阶数; 如果阶数相同则乘 $\log n$.
证明: 先对 $n$ 为 $b^k$, $k\in\mathbb N$ 的情形证明, 下面的渐近符号都是对 $n$ 在 $b^k$ 上的点而言的. 写出递归树,
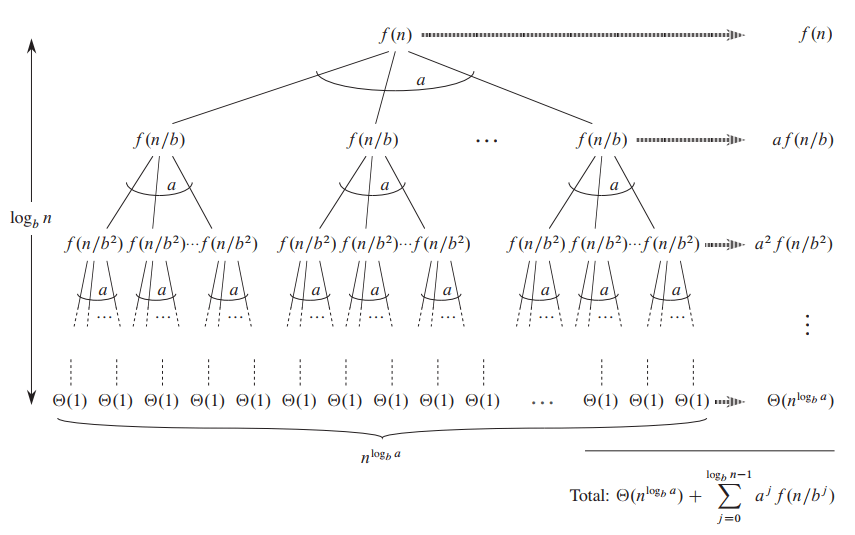
高度为 $\log_b n$, 故有 $a^{\log_b n} = n^{\log_b a}$ 个叶, 从而
\[T(n) = \Theta(n^{\log_b a}) + g(n),\]其中
\[g(n) = \sum_{j=0}^{\log_b n-1}a^j f(n/b^j).\]Case 1. $f(n) = O(n^{\log_b a-\varepsilon})$, 易得 $g(n) = O(n^{\log_b a})$.
Case 2. $f(n) = \Theta(n^{\log_b a})$, 易得 $g(n) = \Theta(n^{\log_b a} \log_b n) = \Theta(n^{\log_b a} \log n)$.
Case 3. 首先 $g(n) = \Omega(f(n))$. 又 $af(n/b)\le cf(n)$ for some constant $c<1$ and sufficiently large $n$. 即 $a^j f(n/b^j) \le c^j f(n)$. 得
\[\begin{align*} g(n) &= \sum_{j=0}^{\log_b n-1}a^j f(n/b^j)\\ &\le \sum_{j=0}^{\log_b n-1}c^j f(n) + O(1)\\ &\le f(n)\sum_{j=0}^\infty c^j + O(1)\\ &=O(f(n)). \end{align*}\]故 $g(n)=\Theta(f(n))$.
对一般的 $n$ 证明略.
Substitution Method
一个粗糙的方法是 substitution method: 首先猜一个阶, 然后验证这个阶是正确的.
例如对
\[T(n) = 2T(n/2) + 1,\]想验证 $T(n) = O(n)$, 即存在 $c>0$ 和 $N$, 对任意 $n>N$, 成立 $T(n) \le cn$, 代入迭代式,
\[\begin{align*} T(n) &\le 2c\frac n2 + 1\\ & = cn + 1, \end{align*}\]其中 $+1$ 这一项因为是关于主项 $n$ 的无穷小项, 所以总是可以想办法消除掉的 (所以可以不管), 例如设
\[T(n) \le cn - d,\]其中 $d\ge 1$, 则
\[T(n) \le cn-2d+1 \le cn-d,\]也就验证了 $T(n) = O(n)$.
一种错误
\(T(n) = 2T(n/2) + n,\) 若猜测 $T(n) = O(n)$, 代入 $T(n) \le cn$, 则 $T(n) \le cn + n$, 主项的常数对不上, 也就没有证明 $T(n) = O(n)$.
变量代换
\(T(n) = 2T(\sqrt n) + \log_2 n,\) 令 $m = \log_2 n$,
\[T(2^m) = 2T(2^{m/2}) + m,\]再令 $S(m) = T(2^m)$.
证明主定理
以 case 1 为例, 先证明 $T(n) = O(n^{\log_b a})$. 易知
\[\begin{align*} T(n) &\le ac \left( \frac{n}{b} \right)^{\log_b a} + f(n)\\ &= cn^{\log_b a} + f(n), \end{align*}\]主项对上了, 所以 $T(n) = O(n^{\log_b a})$, 反过来易知 $T(n) = \Omega(n^{\log_b a})$.
参考
Leiserson, C. E., Rivest, R. L., Cormen, T. H., & Stein, C. (2009). Introduction to algorithms (3rd ed.). Cambridge, MA: MIT press. pp. 83-106