主要参考
- 结城浩. (2014). 图解密码技术 (周自恒, 译). 人民邮电出版社.
不讲数学, 只记概要.
密码
常识
- 不要使用保密的密码算法.
- 算法的秘密早晚会公诸于世. 依靠对算法本身进行保密来确保安全性的行为称为隐蔽式安全性 (security by obscurity). 一旦算法暴露, 那么这种密码系统就崩了.
- 开发高强度的密码算法是非常困难的. 将算法详细信息和源代码交给专业密码破译者, 并为其提供大量的明文和密文样本, 仍然需要花相当长时间破译, 就说明是高强度密码.
- 使用低强度的密码比不进行任何加密更危险. 用户容易通过密码获得一种错误的安全感, 从而麻痹大意.
- 任何密码总有一天会被破解. 严格来说, 一次性密码本 (one-time pad) 是不会被破解的, 但它并不是现实可用的算法.
- 密码只是信息安全的一部分. 人可能才是最脆弱的环节.
对称密码
加密和解密使用的密钥相同, 所以有密钥配送的问题 (key distribution problem).
现实中是有可用的对称密码算法的, 并且今后对称密码也不会消失. 一般来说, 在采用具备同等机密性的密钥长度的情况下, 公钥密码的处理速度只有对称密码的几百份之一. 因此公钥密码并不适合用来对很长的消息内容进行加密. 有时会把两种密码搭配使用.
常会用到 XOR 运算, 因为这是幂等运算.
一次性密码本的原理是 “将明文与一串随机的比特序列进行 XOR 运算”. 关键在于其完全随机, 明文中所有可能的排列组合都会出现, 我们 无法判断哪个是正确的明文, 因此不可破解. 即使遍历了所有可能的密钥, 也无法判断得到的是否是正确的明文. 但是下列问题导致其根本不可用.
- 它的长度和明文相同 (并且由于完全随机, 不可压缩). 保存密钥的难度和保存明文一样, 丢弃密钥就等同于丢弃明文. 首先就没有使用这种加密方法的必要.
- 还是一样的问题, 通信过程中不能处任何差错, 否则就无法解密.
- 密钥的生成不能通过计算机程序生成的伪随机数, 而必须是无重现性的真正随机数.
公钥密码
有若干解决密钥配送问题的方法
- 事先共享密钥. 除了面对面交付, 不一定有安全的共享方式; 另外, 每一个参与传递信息的人都要互相共享密钥.
- 密钥分配中心
- Diffie-Hellman 密钥交换
- 公钥. 最著名的是 RSA, 简洁但强大.
RSA 原理众所周知, 略. 一旦发现了对大整数进行质因数分解的高效算法, RSA 就能被破译.
公钥虽然解决了密钥配送问题, 但是还需要判断得到的公钥是否正确合法 (公钥认证问题), 以防范中间人攻击 (即在传递公钥时, 中间人取而代之传递自己的公钥, 从而使自己能查看/篡改信息).
混合密码系统
用对称密码对消息加密, 然后用公钥密码对对称密码的密钥 (称为会话密钥, 用伪随机数生成器生成) 进行加密. 用对称密码提高速度, 用公钥密码保护回话密钥.
网络上的密码通信所使用的 SSL/TLS 都运用了混合密码系统.
认证
单向散列函数
单向指无法反推.. 以 SHA-256 为例, 输出的散列值长度固定为 256 比特. 这个输出也叫消息摘要或指纹 (fingerprint).
可以用于检验文件的完整性 (integrity), 或者叫一致性. 比如镜像网站发布软件的时候.
SHA-256, SHA-384, SHA-512 这三种哈希函数合起来统称为 SHA-2. SHA-1 已被攻破, SHA-2 尚未被攻破. 另外, SHA-3 也是安全的.
消息认证码
消息的认证 (authentication) 指的是 “消息来自正确的发送者”.
消息认证码 (MAC, message authentication code) 是一种确认完整性并进行认证的技术. 输入包括消息和一个发送者与接收者之间共享的密钥, 输出固定长度的数据, 称为 MAC 值. 如所述, 有密钥配送的问题.
无法解决的问题
- 对第三方证明. 由于发送和接受方共享密钥, 无法向第三方证明到底是谁发的.
- 防止否认 (nonrepudiation). 同上.
数字签名和证书
用发送者的私钥对消息 “加密” 生成签名, 用公钥验证签名. 其实无需对整个消息签名 (加密), 只要先算出消息的哈希值, 在对其签名即可.
同样需要防范针对公钥的中间人攻击, 要知道公钥是否真正属于发送者 (用证书 check).
公钥证书 (public-key certificate) 记载个人信息以及属于此人的公钥, 并由认证机构 (CA, certification authority), “可信的第三方”, 施加数字签名.
应用技术
密钥
访问 https 开头的网页时, Web 服务器和浏览器之间会进行基于 SSL/TLS 的加密通信. 通信中所使用的密钥是仅限本次通信的一次性密钥, 称为会话密钥 (session key).
尽管生成伪随机数的算法有很多种, 但密码学用途的伪随机数生成器必须是专门针对密码学用途而设计的.
Diffie-Hellman 密钥交换
通信双方仅通过交换一些可以公开的信息就能够生成出共享的密钥.
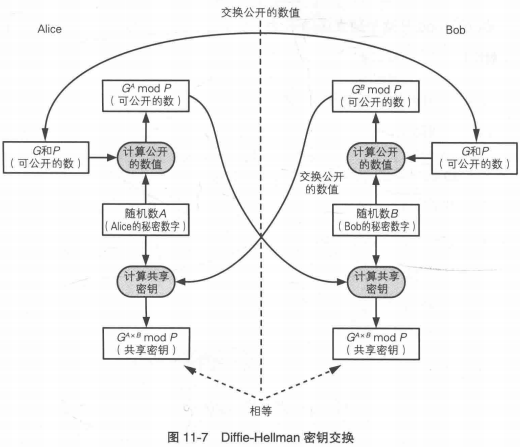
另外还有椭圆曲线 Diffie-Hellman 密钥交换.
基于口令的密码
基于口令的密码 (PBE, password based encryption)
- 生成 KEK. 用伪随机数生成器生成一个称为盐 (salt) 的随机数, 将盐和口令作为输入得到哈希值, 作为加密密钥的密钥 (KEK). 盐是一种防御字典攻击的机制. 字典攻击是一种 事先 进行计算并准备好候选密钥列表的方法. 加盐会让候选 KEK 数量变得巨大.
- 用伪随机数生成器生成会话密钥并加密. 然后就可以丢弃 KEK 了.
- 加密消息.
其中盐和 “用 KEK 加密的会话密钥” 需要安全保存.
随机数
要给随机数下一个严密的定义是非常困难的, 有时甚至会进入哲学争论的范畴.
- 随机性: 不存在统计偏差, 完全杂乱.
- 不可预测性: 不能从过去的数列推测下一个出现的数.
- 不可重现性: 除非将数列本身保存下来, 否则不能重现相同的数列.
越往下越严格. 密码学至少要求不可预测性. 不可预测性是通过使用其他的密码技术来实现的. 仅靠软件是无法生成出具备不可重现性的随机数列的. 软件只能生成伪随机数列, 这是因为运行软件的计算机本身仅具备有限的内部状态.
线性同余法 (linear congruential method) 是一种使用很广泛的伪随机数生成器算法. 然而, 它并不能用于密码技术. 只要谨慎选择参数, 就能够很容易地生成具备随机性的伪随机数列 (周期短).
使用单向散列函数可以编写出能够生成具备不可预测性的伪随机数列.
伪随机数生成器也是会被攻击的.
SSL/TLS
Secure socket layer 和 transport layer security 是世界上应用最广泛的密码通信方法.
- 机密性. 用对称密码, 通过公钥密码或 D-H 密钥交换发送对称密码的密钥.
- 完整性. 用消息认证码 (哈希函数).
- 认证. 公钥加数字签名生成整数.
具体协议内容略.