主要参考
- Boyd, S., & Vandenberghe, L. (2004). Convex optimization. Cambridge university press.
凸优化最有名 (?) 且十分易读的教材, 附录有一些线性代数的回顾. 如果不打算全读, 只读每章开头的小节可以很快地理清脉络.
如无额外说明, 图片均出自本书.
部分没有解释的概念不太影响主线故事, 可以查书看定义也可以忽略.
辅助参考
- Nocedal, J., & Wright, S. (2006). Numerical optimization. Springer Science & Business Media.
很有名也写得很好的数值优化教材. 当字典查.
凸性
符号约定
符号都是标准的, 大写字母表示矩阵或集合, 小写字母表示列向量. 其余符号都在行文中说明.
函数的定义域默认为使函数有意义的变量可取的最大集合, 比如 $f(x) = \log x$ 的定义域默认为 $\operatorname{dom} f = (0, \infty)$. 为了符号简便, 不妨将函数延拓为广义实值函数 (即可取 $\pm\infty$), 即
\[\begin{align*} \tilde f(x) = \begin{cases} f(x), & x\in \operatorname{dom} f, \\ \infty, & x\notin\operatorname{dom} f. \end{cases} \end{align*}\]于是, $\operatorname{dom} f = \{x \mid \tilde f(x) < \infty \}$, 这样以后就不用再特意强调函数的定义域.
符号 $\nabla f$ 为 $f$ 的梯度 (取为列向量), $\nabla^2 f$ 为 Hesse 矩阵. 右上角的 ‘ 指矩阵转置.
优化问题
优化问题的一般形式
\[\begin{align*} \text{minimize} &\quad f_0(x) \\ \text{subject to} &\quad f_i(x) \le 0, \quad i=1,\dots, m. \end{align*}\]其中 $x=(x_1, \dots, x_n)’$ 称为优化变量, $f_i\colon\mathbb R^n \to \mathbb R$, $i=1,\dots, m$ 为约束函数, 要最小化目标函数 $f_0\colon\mathbb R^n \to \mathbb R$.
凸优化是指上述函数都是凸的 (包含了其定义域也是凸的, 后详).
满足所有约束的向量称为可行解. 最优值 (不一定能取到) 定义为
\(p^\ast = \inf\{ f_0(x) \mid f_i(x) \le 0, \, i=1,\dots, m\}.\) 约定 $\inf \varnothing = \infty$, 即问题不可行 (没有可行解) 时最优值为无穷大. 若 $p^\ast = -\infty$, 称问题无下界 (unbounded below).
如果向量 $x^\ast$ 可行且 $f(x^\ast) = p^\ast$, 则称 $x^\ast$ 为最优解 (不一定唯一).
The challenge, and art, in using convex optimization is in recognizing and formulating the problem. Once this formulation is done, solving the problem is, like least-squares or linear programming, (almost) technology. (Boyd & Vandenberghe, 2004, p. 8)
神经网络是复杂的非凸优化问题, 而经典的统计问题大多是凸优化问题. 凸优化在非凸优化中也有相当地位, 可以参考 覃含章的回答 和 Ormsom 的回答.
凸集
如果在集合中任取两点连成的线段都完全落在那个集合中, 那么这个集合称为凸集. 即集合 $C$ 是凸的, 若对任意 $x, y \in C$, 对任意 $0\le \theta \le 1$, 都有
\[\theta x + (1-\theta)y \in C.\]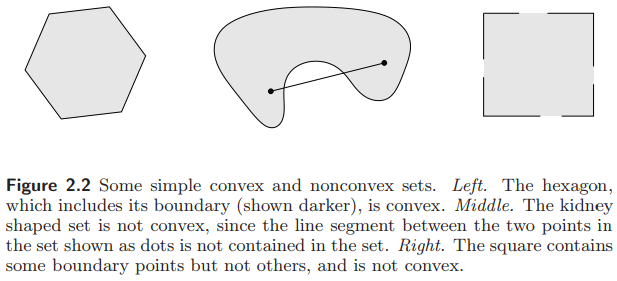
凸函数
函数 $f$ 是凸的当且仅当它的上图 (epigraph)
\[\operatorname{epi} f = \{ (x, t) \mid f(x)\le t \}\]是凸的.
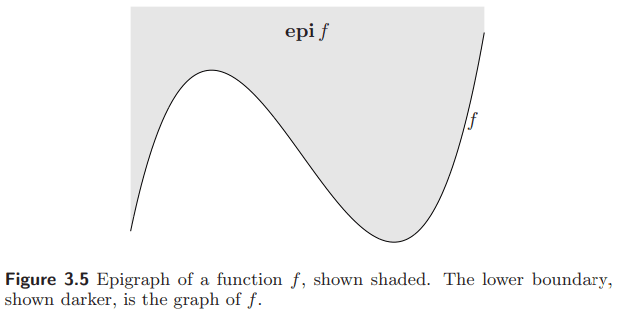
等价地, 凸函数通常定义为, $f$ 是凸的, 若定义域是凸的, 且对任意 $x$, $y$, 和任意 $0 \le \theta \le 1$, 都有 (Jensen 不等式)
\[f(\theta x + (1-\theta)y) \le \theta f(x) + (1-\theta)f(y).\]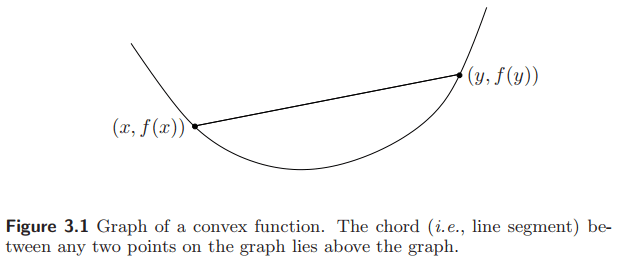
很容易推广到概率测度上, $f(\mathbb E X) \le \mathbb E f(X)$.
如果 $-f$ 是凸的, 则称 $f$ 为凹的.
凸优化问题
回忆优化问题一节的记号, 一个等式约束可以由两个不等式约束得到. 由于所有函数都要是凸的, 这意味着等式约束函数既是凸的又是凹的, 故必为仿射函数 (证明可参考 这里 Theorem 2).
注: 线性变换为 $x \mapsto Ax$, 仿射变换 $x \mapsto Ax + b$, 在其他领域中后者有时也被称为线性变换.
对偶
Lagrange 对偶
考虑优化问题 (不要求为凸).
\[\begin{align*} \text{minimize} &\quad f_0(x) \\ \text{subject to} &\quad f_i(x) \le 0, \quad i=1,\dots, m,\\ &\quad h_i(x) = 0, \quad i=1,\dots, p, \end{align*}\]Lagrange 对偶的基本想法是把约束加权放入目标函数中, Lagrange 函数 为
\[L(x, \lambda, \nu) = f_0(x) + \lambda'f(x) + \nu' h(x),\]其中 $\lambda = (\lambda_1, \dots, \lambda_m)’$, $\nu = (\nu_1, \dots, \nu_p)’$ 为 Lagrange 乘子, $f(x) = (f_1(x), \dots, f_m(x))’$, $h(x) = (h_1(x), \dots, h_p(x))’$.
对偶函数 为
\[g(\lambda, \nu) = \inf_x L(x, \lambda, \nu).\]对偶函数给出了最优值 $p^\ast$ 的下界: 对任意 $\lambda \succeq 0$ 和任意 $\nu$, 有 $g(\lambda, \nu) \le p^\ast$ (因为新加的带乘子的两项都不大于零).
对偶问题 就是找原始问题最优值最好的下界, 且是个凸优化问题 (因为对偶函数是关于 $(\lambda, \nu)$ 的仿射函数的点点极小值, 所以一定是凹的, 即使原问题不是凸的)
\[\begin{align*} \text{maximize} &\quad g(\lambda, \nu) \\ \text{subject to} &\quad \lambda \succeq 0. \end{align*}\]记它的最优值 (对偶最优) 为 $d^\ast$, 称 $p^\ast - d^\ast (\ge 0)$ 为对偶间隙. 如果对偶间隙为 0, 则称为强对偶, 意味着原始问题和对偶问题最优值相等. 如果原问题是凸优化, 则通常有强对偶, 因此可以利用对偶问题求解.
KKT 条件
解优化问题可以转化为解 KKT 条件.
假设所有函数都可微 (不用假设凸性). 假设 $x^\ast$ 是原问题最优解, $(\lambda^\ast, \nu^\ast)$ 是对偶问题最优解.
因为 $x^\ast$ 是 $L(x, \lambda^\ast, \nu^\ast)$ 关于 $x$ 的最小值点, Lagrange 函数关于 $x$ 的偏导在该点一定为零 (假设函数可微从而定义域为开集). 如果问题强对偶, 由对偶函数的形式可知 $\lambda_i f_i(x)$ 一定为零 (互补松弛). 组合起来, 如果问题强对偶, 则原始问题和对偶问题的最优解一定满足 Karush-Kuhn-Tucker (KKT) 条件: Lagrange 函数梯度为零, 原始可行, 对偶可行, 互补松弛.
\[\begin{align*} \nabla f_0(x^\ast) + {\lambda^\ast}'\nabla f(x^\ast) + {\nu^\ast}'\nabla h(x^\ast) &=0,\\ f_i(x^\ast) &\le 0, \quad i=1,\dots, m,\\ h_j(x^\ast) & = 0, \quad j=1,\dots, p,\\ \lambda^\ast_i &\ge 0, \quad i=1,\dots, m,\\ \lambda^\ast_i f_i(x^\ast) & = 0, \quad i=1,\dots, m. \end{align*}\]对于强对偶的凸优化问题, 一组解是最优解当且仅当它们满足 KKT 条件 (只需注意到凸函数达到最优当且仅当导数为零).
If a convex optimization problem with differentiable objective and constraint functions satisfies Slater’s condition (保证问题强对偶), then the KKT conditions provide necessary and sufficient conditions for optimality: Slater’s condition implies that the optimal duality gap is zero and the dual optimum is attained, so $x$ is optimal if and only if there are $(\lambda, \nu)$ that, together with $x$, satisfy the KKT conditions. (Boyd & Vandenberghe, 2004, p. 244)
求解算法
算法有很多, 主要目标是讲简化版的 barrier method, 所以要先提一下 Newton 法.
Newton 法: 无约束和等式约束问题
想法是在当且迭代点 $x_k$ 用二次函数逼近原来的目标函数. 替换后的问题很容易解析地求解, 而这个解 $x_k + \Delta x_k$ 又能作为原始问题解的估计. 记第 $k$ 次迭代的点为 $x_k$, 令 $x_{k+1} = x_k + \Delta x_k$.
考虑无约束凸优化问题 $\min_x f(x)$. 假设 $\nabla^2 f(x)$ 存在且正定. 用二阶 Taylor 展开 $\hat f$ 近似 $f$,
\[\hat f(x+v) = f(x) + \left(\nabla f(x)\right)' v + \frac12 v' \nabla^2 f(x) v,\]这是关于 $v$ 的凸二次函数, 当 $v = -\left(\nabla^2 f(x)\right)^{-1}\nabla f(x)$ 时达到极小. 取这个 $v$ 作为 Newton 步 (迭代的更新方向) $\Delta x$, 则 $x+\Delta x$ 是 $\hat f$ 的极小值点, 也应该是 $f$ 最优解的很好的估计.
另一种视角 假设 $f$ 为凸且可微, 则 $x^\ast$ 是最优解的充要条件是 $\nabla f(x^\ast) = 0$. 这就把优化问题转化为了方程求根问题.
假设 $x$ 在 $x^\ast$ 附近, 用 Taylor 展开线性逼近它的梯度
\[\nabla f(x+v) \approx \nabla f(x) + \nabla^2 f(x) v = 0,\]取 $\Delta x = v = -\left(\nabla^2 f(x)\right)^{-1}\nabla f(x)$ 作为 Newton 步, 则 $x+\Delta x$ 是 $x^\ast$ 很好的逼近.

Newton decrement
\[\lambda(x) = \{(\nabla f(x))'\left(\nabla^2 f(x)\right)^{-1}\nabla f(x)\}^{1/2}\]称为 Newton decrement, 因为
\[f(x) - \inf_y \hat f(y) = f(x) - \hat f(x+\Delta x) = \frac12 \lambda(x)^2.\]于是 $\lambda/2$ 就是 $f(x) - p^\ast$ 的一个估计, 可以作为停止条件.

收敛性分析略.
等式约束 对等式约束凸优化
\[\begin{align*} \text{minimize} &\quad f_0(x) \\ \text{subject to} &\quad Ax = b, \end{align*}\]类似地, 用二阶 Taylor 展开逼近目标函数, 得到关于 $v$ 的优化问题 (强对偶)
\[\begin{align*} \text{minimize} &\quad \hat f(x+v) = f(x) + (\nabla f(x))' v + (1/2)v'\nabla^2 f(x) v \\ \text{subject to} &\quad A(x+v) = b. \end{align*}\]求解 KKT 条件 (关于 $\Delta x$ 和 $\nu$ 的方程)
\[\begin{align*} \nabla f(x) + \nabla^2 f(x)\Delta x + A' \nu &= 0,\\ A\Delta x &= 0 \end{align*}\]可以得到 $\Delta x$ 作为 Newton 步 (假设有解), 其中 $\nu$ 是对偶变量. 之后的做法同前面的 Newton 法.
内点法: 不等式约束问题
内点法是一类求解凸优化问题的方法, 因为要求每次迭代都严格满足不等式约束 (从而落在可行域的 relative interior) 而得名.
考虑下述不等式约束凸优化问题
\[\begin{align*} \text{minimize} &\quad f_0(x) \\ \text{subject to} &\quad f_i(x) \le 0, \quad i=1,\dots, m,\\ &\quad Ax = b, \end{align*}\]其中 $f_i\colon \mathbb R^n \to \mathbb R$ 凸且二次连续可微.
假设存在最优解 $x^\ast$, 记最优值为 $p^\ast = f_0(x^\ast)$.
假设问题严格可行, 即存在可行的 $x$ 使得 $f_i(x) < 0$. 这意味 Slater 条件成立, 因此强对偶成立, 存在对偶最优解 $\lambda^\ast$, $\nu^\ast$, 并且和最优解 $x^\ast$ 成立 KKT 条件.
例如对于凸二次规划, KKT 条件是充要条件, 见 Nocedal & Wright (2006) Theorem 16.4.
Barrier method
想法是把不等式约束问题近似为一个等式约束问题, 再用 Newton 法求解. 首先把等式约束拿到目标函数里.
\[\begin{align*} \text{minimize} &\quad f_0(x) + \sum_{i=1}^m I_-(f_i(x)) \\ \text{subject to} &\quad Ax = b, \end{align*}\]其中
\[I_-(u) = \begin{cases} 0, & u\le 0, \\ \infty, & u > 0. \end{cases}\]现在问题是目标函数不可微, 于是用相近的对数函数 (称为 logarithmic barrier)
\[\hat I_-(u) = -(1/t)\log(-u)\]替换 $I_-(u)$. 其中 $t>0$ 是参数, 越大则逼近越准确. 上述函数凸, 递增, 可微.
对每个 $t>0$, 上述问题最优解记为 $x^\ast(t)$ (假设存在唯一的解, 细节略), 这族向量称为中心路径 (随着 $t$ 变换, $x(t)$ 从图像上看起来是条路径). 可知其严格可行 (因为目标函数里有 log 函数), 且存在 $\hat \nu(t)$, 使得 Lagrange 函数导数为 0:
\[\nabla f_0(x^\ast(t)) + \sum_{i=1}^m \frac{1}{-tf_i(x^\ast(t))}\nabla f_i(x^\ast(t)) + A' \hat\nu(t) = 0.\]可知每个最优解都对应了原始问题的对偶可行解 (因为 $x^\ast(t)$ 是凸函数的导数的驻点, 意味着它最小化), 根据上式可取 $\lambda^\ast_i(t) = -1/(tf_i(x^\ast(t)))$, 于是对偶函数
\[g(\lambda^\ast(t), \nu^\ast(t)) = f_0(x^\ast(t)) - m/t.\]故对偶间隙不大于 $m/t$. 对当前参数 $t$, 问题的最优值和原始问题的最优值的差不大于这个间隙:
\[f_0(x^\ast(t)) - p^\ast \le m/t,\]所以当 $t\to\infty$ 时, $x^\ast(t)$ 收敛于最优点.

另外还有 primal-dual interior-point methods, 和 barrier method (也叫 path-following method) 的区别在于求解 Newton 步的方式略有不同 (见 Boyd 书 11.3.4 Newton step for modified KKT equations, 和 11.7.1 Primal-dual search direction).
Primal-dual interior-point methods are often more efficient than the barrier method, especially when high accuracy is required, since they can exhibit better than linear convergence. For several basic problem classes, such as linear, quadratic, second-order cone, geometric, and semidefinite programming, customized primaldual methods outperform the barrier method. (Boyd & Vandenberghe, 2004, p. 609)
