Months ago I came across an article on the methods of shuffling cards in TCG tournaments. Given limited time in a match, the author, hyakkoTCG@hyakko_tcg sought a way to mix a deck thoroughly by shuffling three times. However, at least to me, it is obvious that the methodology proposed is fundamentally flawed. Later I found out in surprise that the article was widely disseminated: it got 2.3k retweets and 3.1k likes on twitter. It also began to spread on Weibo, so I wrote a short refutation in Chinese immediately. Though it was a bit late, I still decided to write another one in English so that I can send it to Hyakko.
I avoided introducing fancy math in the hope that average readers can follow. If you have difficulty reading in English, you may resort to Google translation. Normally when the source language is English, Google should do a good job.
I don’t have time to write carefully. It would appreciated if you can tell me any mistake I made. And feel free to drop a comment if you have any question.

Restatement
The article, あなたのそのシャッフル、本当に混ざっていますか? (Is your shuffling method really mixing cards thoroughly?), is Hyakko’s undergraduate thesis. Only the outline is provided, but it seems that there are no more interesting details to be supplemented. He attempted to find an approach to randomizing a deck by shuffling three times on account of limited time in a real match. Without loss of generality, the deck is assumed to consist of 40 cards. Below I will briefly restate his article.
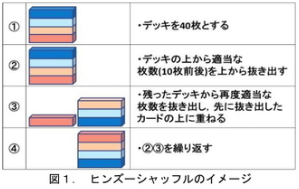
Shuffles. Two types of shuffles, the riffle shuffle and the Hindu shuffle (overhand shuffle), were considered. One may easily find videos to see how they are executed in reality. Mathematically, the riffle shuffle can be well approximated by the Gilbert–Shannon–Reeds model. When conducting a riffle shuffle, first the deck is cut into two packets and then packets are interleaved together randomly.

Considering the card sleeves, Hyakko modified GSR model to ensure that no more than 4 consecutive cards from the same packet will appear in the middle of a shuffled deck. We can see from the figure above that 4 consecutive cards from the right packet appear in the shuffled deck.
このように片方から重なりすぎることもあります。が、TCGではスリーブの関係上その確率がかなり低いです。”今回は4回以上連続して重ならない”としてプログラムを組んでいます。
For Hindu shuffle, Hyakko modeled it in this way: put the top 7-12 (where the number is chosen randomly) cards of the deck to another pile repeatedly until the deck is exhausted and the new pile then becomes the deck after one Hindu shuffle.
ヒンズーシャッフルは抜き出す枚数を7から12枚としてシャッフルのアルゴリズムを再現した。(From Section 5 of Hyakko’s outline.)
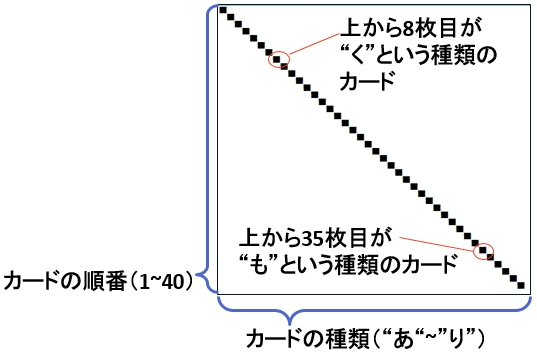
Experiments. Recall that we only shuffle three times. Hyakko experimented all combinations of the two shuffles: RRR, RRH, …, HHH, there are 8 in total, with R and H representing riffle and Hindu respectively. For every shuffle combination (e.g. RRH), a 40 times 40 matrix, denoted as $M = (m_{i, j})$, or to be verbose,
\[M = \begin{pmatrix} m_{1,1} & m_{1,2} & \dots & m_{1, 40}\\ m_{2,1} & m_{2,2} & \dots & m_{2, 40}\\ \vdots & \vdots & \ddots & \vdots\\ m_{40,1} & m_{40,2} & \dots & m_{40, 40} \end{pmatrix},\]is used to record results of simulations. For initialization, $M=0$, i.e. $m_{i,j}=0$ for any $i$, $j$. After one shuffling simulation (in this example, RRH indicates that two riffle shuffles followed by one Hindu shuffle are conducted in one simulation), if a card with index $j$ (the $j$-th card counted from the top) is moved to index $i$, then the entry $m_{i,j}$ is incremented by 1. Thus, $m_{i,j}$ records the total times when $j$-th card is moved to $i$-th position in simulations, and Hyakko named it “重複回数 (number of duplicates)”.
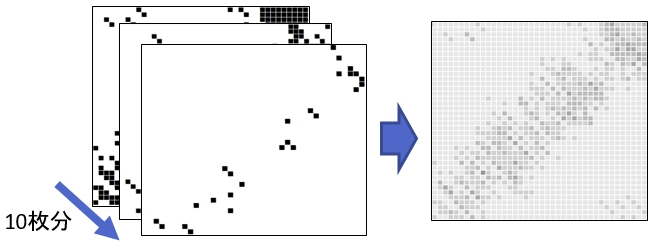
Evaluation. In ideal case, for any card, there is 1/40 chance that it is moved to any position after shuffling. Hyakko simulated every shuffle combination for 100 times, and focused on the total count of 2s and 3s in the matrix, since 100/40 = 2.5, which means that the expectation of $m_{ij}$ is 2.5 ideally. (There are 1600 entries in a matrix. If there are, say, 402 twos and 200 threes, then total count is 602.)
例えば40枚のカードがちゃんと混ざった場合、ある一枚のカードが一番上になる確率っていくつでしょう?
40分の1ですよね?
40回に1回その位置にあれば混ざってるといえると思います。
つまり今回100回行ったので2回か3回重なってればいいわけです。
Observing the total count for HRR is the highest, Hyakko concluded that HRR is the best shuffling method among the 8 combinations. In addition, he visualized the matrix to show that cards are mixed up virtually.

Rufutation
A discerning reader might have noticed the above paragraphs are full of holes, and I shall point out a few.
Invalid Evaluation
First I’m going to talk about the crux of the matter, the evaluation. Although there is no hard-and-fast rule to measure the performance of a shuffling method, the “number of duplicates” is simply not an appropriate one. Consider a new shuffle (call it cut shuffle) as follows:
- Randomly select a card from the deck. Every card is chosen with probability 1/40.
- Suppose the selected card is the $i$-th from the top, then the top $i$ cards are moved to a new pile, then the rest of the cards are put onto the new pile.
So this is just the Hindu shuffle with only one cut. And it is obvious that for any card, there is 1/40 chance that it is moved to any position after one cut shuffle, which implies that the cut shuffle might be favored by “number of duplicates” criterion. The code in the appendix supports my conjecture. However, as anyone knows, this cut shuffle is undesired.
Another problem is that, though the expectation of $m_{i,j}$ is 2.5, it doesn’t necessarily mean the probability of $m_{i,j}$ being 2 or 3 is highest. The argument given by Hyakko is insufficient. Even when we assume the probability being 2 or 3 is the highest, it still doesn’t make any sense to track the total counts of them. What numbers are you going to track if there are more than 100 simulations?
Further Explanation
According to MTG rules,
Decks must be randomized at the start of every game and whenever an instruction requires it. Randomization is defined as bringing the deck to a state where no player can have any information regarding the order or position of cards in any portion of the deck.
The phrase “order or position” is key. A deck that is “mana-weaved” is not random; even though the player may have no information about the location of a specific card, they have information about the cards’ order (that is, land-spell-spell, land-spell-spell). Also key is that a player shouldn’t know any information on where a card is, not even which half of the deck it is in.
The “number of duplicates” completely disregards the “order” (recall the cut shuffle example), and therefore is uninformative. And you can’t tell by it whether the shuffling method is closer to the ideal one.
Imagine a deck of 3 cards $a$, $b$, $c$. There are $3!$ possible states for this deck, i.e. $abc$, $acb$, $\dots$, $cba$. A shuffle is a permutation (a function) that maps the deck from one state to another, and the permutation is chosen randomly according its distribution. Here the distribution of permutations means “by what probability will one specific permutation occurs”. There are totally $40!$ permutations, the same with the number of deck states. In fact, the “number of duplicates” criterion only reflects a little information of the distribution of permutations that a shuffling method is related to.
When we say a deck is randomized in a mathematical sense, we usually mean any of $40!$ states may appear with same probability. This situation can only hold when each permutation occurs with probability $1/40!$ (uniform distribution). And I will call this kind of shuffle, the ideal shuffle. If the shuffle is ideal, “for any card, there is 1/40 chance that it is moved to any position”, but the reverse is not true (the cut shuffle is an example).
If you are not familiar with probability theory, you can skip ahead to the next section without loss of continuity. To formulate the point previously noted, a shuffle is a random variable $\xi\colon \Omega \to S$ where $\Omega$ is the sample space and $S$ is the set of all permutations (the symmetric group). And we are actually considering the distribution of $\xi$.
Given the description above, one viable solution is to measure the difference between the uniform distribution and the distribution of permutations induced by the proposed shuffling method. There are various approaches to address this problem, but all are non-trivial. There also exist other ways to assess randomness. For more details, readers are referred to the literatures and pages listed in the appendix.
Poor Experiments
In the following sections, bear in mind that I will pretend that “Hyakko’s evaluation is valid”, and show flaws in other perspectives.
Hyakko’s experiments are rather primitive. There is no control group, which can be introduced by executing ideal shuffles in this case. No convincing conclusions can be drawn without proper contrast.
To make matters worse, he only conducted simulations $8\times 100$ times, which is in no way adequate. Since his description is vague, I don’t know how Hyakko implemented shuffles exactly. I implemented shuffles with my own understanding and surmise, and I don’t think it will be a big issue in principle.
As a result, it took me less than 0.3 second to replicate his scheme. I also noticed that the “number of duplicates” for all shuffles of my implementation didn’t align with Hyakko’s at all, especially the counts for $m_{i,j}=0$ or $m_{i,j}$ taking large values, which is rather weird. At least I can guarantee that the ideal shuffle and the GSR model are implemented correctly, and that the modified riffle shuffle behaves similarly with the GSR model. Any way I will report results with my implementation.
With a little refinement, I repeated his experiments 500 times ($500\times 100$ times for every shuffle combination). It is shown that by “number of duplicates” criterion, rather than HRR as Hyakko claimed, RRR is the best shuffling method among the 8 combinations, C (for cut shuffle) is much better than RRR, and CCC even “beats” the ideal shuffle. Below S and G stand for the ideal shuffle and the GSR model, respectively.
CCC 768.24
GGGGGGG 760.678
S 760.478
C 756.08
GGG 709.41
RRR 708.784
HRR 699.648
RHR 651.226
HHR 644.764
RRH 601.118
HRH 580.214
RHH 437.426
HHH 400.494
Each method for 500*100 times
Elapsed Time: 314.96s

You may skip to the next section safely.
To give some insight, if “for any card, there is 1/40 chance that it is moved to any position”, then $m_{i,j}$ is binomially distributed, i.e.
\[\mathbb P(m_{i,j} = k) = \begin{pmatrix}40 \\ k\end{pmatrix}\left(\frac{1}{40}\right)^k\left(\frac{39}{40}\right)^{n-k},\]where $n$ is the number of simulations. In this case, $n=100$, and for any $i$, $j$,
\[\begin{align*} \mathbb P(m_{i,j} = 1) = 0.204,\\ \mathbb P(m_{i,j} = 2) = 0.259,\\ \mathbb P(m_{i,j} = 3) = 0.217.\\ \end{align*}\]By lineality of expectation, we can predict that the expectation of total counts of 2s and 3s should be $1600\times (0.259+0.217) = 761.6$, which agrees with my result.
Unjustified Results
You may skip this section.
It could be argued that the cut shuffle proposed previously is not realistic. In this section, I will illustrate the defects of Hyakko’s article in another perspective. Recall that
Observing the total count for HRR is the highest, Hyakko concluded that HRR is the best shuffling method among the 8 combinations.
His reasoning is untenable. One should interpret the simulation results in terms of probabilities, rather than certainties.
Following Hyakko’s thought, we are going to test whether “for any card, there is 1/40 chance that it is moved to any position” after shuffling.
- For any card, i.e. for any column $j$, $(m_{1, j}, \dots, m_{40,j})$ should be generated by a multinomial distribution with $p_1=\cdots=p_{40}$.
- For any position, i.e. for any column $i$, $(m_{i,1}, \dots, m_{i,40})$ should be generated by a multinomial distribution with $p_1=\cdots=p_{40}$.
The following test is improvised: we test the 80 sequences by 80 Chi-squared tests, and see how many p-values are less than 0.05. This is not an appropriate test but should serve as a sanity check to rule out some apparently unreliable methods. The results are as follows.
C 0
CCC 0
S 6
GGGGGGG 26
GGG 57
RRR 66
HRR 77
RRH 80
RHR 80
RHH 80
HRH 80
HHR 80
HHH 80
Each method for 50000 times
Elapsed Time: 174.92s
We can see that the methods proposed by Hyakko are inferior according to this test. As a matter of fact, take HHH for instance, we can analyze as follows:
- We track the top card. After the first Hindu shuffle, the top card is at position 29-34.
- After the second Hindu shuffle, it might be at position 1-23.
- After the third Hindu shuffle, it can’t be at position 1 (the top).
So HHH has serious systematic biases, which result in bad consequences, leaving the deck far from being randomized. Other methods might be analyzed in a similar manner.
Conclusions
Inappropriate methodology leads to misleading results. By any means, Hyakko failed to offer any meaningful conclusions.
I could give extensive details and formulate the problem in rigorous math but I don’t have that time. This post should be enough and I hope I made my point clear.
In fact, riffle shuffle is way better than Hindu shuffle. So to give some suggestions in practice,
- Always use riffle shuffles.
- You may employ riffle shuffles combined with some cut shuffles in reality.
I also skimmed through his references.
This is a restatement of Diaconis’ famous paper.
I didn’t read it much.
Hyakko almost followed this article, which, unfortunately, suffered from similar problems as his did.
Appendix
Recommended Material
For average readers:
For advanced readers:
- Trailing the Dovetail Shuffle to its Lair. by Diaconis. The most famous paper on shuffling. Interesting as its name.
- The cutoff phenomenon in finite Markov chains by Diaconis.
- How many times should you shuffle a deck of cards.. This one should be the easiest to read.
My Implementation
The random seed is set so that readers can reproduce my results.
import time
import numpy as np
from scipy.stats import chisquare
class Deck():
def __init__(self, n_cards=40):
'''
A deck consisting n cards will be presented as [0, 1, ..., n-1]
:param n_cards int: number of cards in the deck
'''
self.cards = np.arange(n_cards)
def riffle_shuffle(self):
'''Gilbert–Shannon–Reeds model'''
tmp = np.random.binomial(n=1, p=0.5, size=len(self.cards))
self.cards = np.array([self.cards[k] for k in np.argsort(np.argsort(tmp, kind='stable'), kind='stable')])
def quasi_riffle_shuffle(self):
'''According to Hyakko's description'''
cut = np.random.binomial(n=len(self.cards), p=0.5)
p1, p2 = 0, cut
packet = -1
streak = 0
flag = 1
cards = []
while p1 < cut and p2 < len(self.cards):
x = cut - p1
y = len(self.cards) - p2
if flag:
if np.random.uniform() >= x/(x+y):
cards.append(self.cards[p2])
p2 += 1
if packet == 0:
flag = 0
streak += 1
packet = 1
else:
cards.append(self.cards[p1])
p1 += 1
if packet == 1:
flag = 0
streak += 1
packet = 0
else:
if np.random.uniform() >= x/(x+y):
if packet:
if streak == 4:
cards.append(self.cards[p1])
p1 += 1
packet = 0
streak = 1
else:
cards.append(self.cards[p2])
p2 += 1
streak += 1
else:
cards.append(self.cards[p2])
p2 += 1
packet = 1
streak = 1
else:
if packet:
cards.append(self.cards[p1])
p1 += 1
packet = 0
streak = 1
else:
if streak == 4:
cards.append(self.cards[p2])
p2 += 1
packet = 1
streak = 1
else:
cards.append(self.cards[p1])
p1 += 1
streak += 1
cards.extend(self.cards[p1:cut])
cards.extend(self.cards[p2:])
self.cards = np.array(cards)
def hindu_shuffle(self):
'''According to Hyakko's description'''
tmp = [0]
s = 0
while s < len(self.cards):
s += np.random.randint(7, 13) # uniform, can be modified here
tmp.append(s)
tmp[-1] = len(self.cards)
idx = []
for i in range(len(tmp)-2, -1, -1):
idx.extend(range(tmp[i], tmp[i+1]))
self.cards = self.cards[idx]
def cut_shuffle(self):
self.cards = np.roll(self.cards, np.random.randint(0, len(self.cards)))
def shuffle(self):
'''ideal shuffle'''
np.random.shuffle(self.cards)
def com_shuffle(self, method='rrr'):
'''
:param method str:
'r' for quasi riffle shuffle,
'g' for riffle shuffle,
'h' for Hindu shuffle,
'c' for cut shuffle,
's' for ideal shuffle
'''
for m in method:
m = m.lower()
if m == 'r':
self.quasi_riffle_shuffle()
elif m == 'g':
self.riffle_shuffle()
elif m == 'h':
self.hindu_shuffle()
elif m == 'c':
self.cut_shuffle()
elif m == 's':
self.shuffle()
else:
raise ValueError('Shuffling method not understood')
def simulation(n_cards=40, method='rrr', n_sim=100):
'''
:param method str: Used in com_shuffle
:param n_sim int: Number of simulations
'''
result = np.zeros([n_cards, n_cards], dtype=int)
for _ in range(n_sim):
deck = Deck(n_cards)
deck.com_shuffle(method)
for loc, card in enumerate(deck.cards):
result[loc][card] += 1
# print(method, dict(zip(*np.unique(result, return_counts=True))))
return np.count_nonzero((result==2)|(result==3)), result
start_time = time.time()
n = 500
n_sim = 100
methods = ['S', 'C', 'G'*7, 'CCC', 'GGG', 'RRR', 'RRH', 'RHR', 'HRR', 'RHH', 'HRH', 'HHR', 'HHH']
records = []
for method in methods:
np.random.seed(0xC7)
s = 0
for _ in range(n):
s += simulation(method=method, n_sim=n_sim)[0]
records.append((method, s/n))
records.sort(key=lambda x:-x[1])
for method, rep in records:
print(method, ' '*(7-len(method)), rep)
print(f'Each method for {n}*{n_sim} times')
print(f'Elapsed Time: {time.time() - start_time : .2f}s')
start_time = time.time()
methods = ['S', 'C', 'G'*7, 'CCC', 'GGG', 'RRR', 'RRH', 'RHR', 'HRR', 'RHH', 'HRH', 'HHR', 'HHH']
n_sim = 50000
alpha = 0.05
record = []
for method in methods:
np.random.seed(0xC7)
_, result = simulation(method=method, n_sim=n_sim)
test = np.concatenate([chisquare(result)[1], chisquare(result.T)[1]])
record.append((method, len(test[test<alpha])))
for method, num in sorted(record, key=lambda x: x[1]):
print(method, ' '*(7-len(method)), num)
print(f'Each method for {n_sim} times')
print(f'Elapsed Time: {time.time() - start_time : .2f}s')