简单复习.
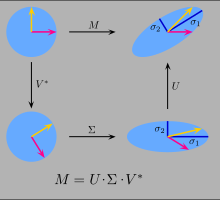
考虑 $m\times n$ 的实矩阵 $A$, 秩为 $r$, 记 SVD (singular value decomposition) 的一般形式为
\[A = U\Sigma V',\]其中 $U=(u_1,\dots,u_m)$, $V=(v_1,\dots,v_n)$ 为正交阵,
\[\Sigma = \begin{pmatrix} S & O\\ O & O \end{pmatrix},\]其中 $S = \text{diag}\{\sigma_1,\dots,\sigma_r\}$, $\sigma_1\ge\cdots\sigma_r> 0$ 是 $A$ 的非零奇异值.
Proof. 由于 $A’A$ 是对称半正定矩阵, 故存在正交对角化
\[A'A = V\Lambda V',\]其中 $V$ 是正交阵, $\Lambda = \text{diag}\{\lambda_1,\dots,\lambda_n\}$, 且特征值非负, 不妨设 $\lambda_1\ge\cdots\ge\lambda_n$.
另外 $r = \text{rank}(A) = \text{rank}(A’A)$. 事实上, $Ax = 0$ 的解都是 $A’Ax = 0$ 的解; 而若 $A’Ay = 0$, 则 $y’A’Ay = 0$ 意味着 $Ay = 0$. 因此只有 $r$ 个非零特征值, 记 奇异值 $\sigma_j = \sqrt{\lambda_j}$.
下面记
\[u_j = Av_j / \sigma_j, \quad j=1,\dots, r.\]显然 $u_1, \dots, u_r$ 是一组单位正交基, 将它扩张为 $m$ 维的单位正交基, 最后整理即得 SVD. $\square$
Note:
- 最后一段也就是说, 对任意 $A$, 在 $r$ 维空间存在一组正交基, 使得其经过 $A$ 映射后为依然为一组正交基.
- 当然了, 把 $U$, $V$ 分别写成 $m\times r$ 和 $n\times r$ 矩阵, $\Sigma$ 为对角线元素全为正的对角阵也行.
- 从 SVD 的形式, $V$ 和 $U$ 表示旋转, 而 $\Sigma$ 表示拉伸, 也就是其几何意义.
- 从 SVD 的形式, $V$ 是 $A’A$ 的正交特征向量, $U$ 是 $AA’$ 的正交特征向量.
把 $A$ 视为 中心化后 的样本矩阵, 每一行为一个样本 ($m$ 个样本), 每一列代表一个特征 ($n$ 个特征). 则样本协方差矩阵为 $A’A/m$, 而主成分 (principal component) $Av_j$ 的样本方差为 $\sigma_j/m$. 奇异值 $\sigma_j$ 越大意味着对应的样本方差越大, 我们把方差大视为提供了更多信息.
$A$ 可写为
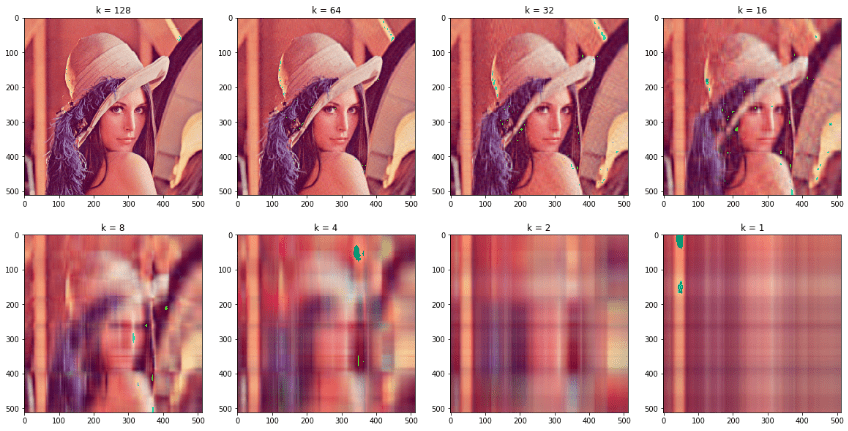
\[A = \sum_{k=1}^r \sigma_k u_kv_k',\]把带有较少信息的小的奇异值扔掉便达到了压缩 (减少需要存储的东西) 的目的, 比如图像压缩.
PCA (principal component analysis) 降维也是同样的. 不过 PCA 还有若干种不同的 formulation.
从几何意义直观的展示就是, 奇异值大的那个轴数据更散布, 从而方差更大.
References
- 姚慕生, 吴泉水, 谢启鸿. (2014). 高等代数学 (第三版). 上海: 复旦大学出版社. pp. 414-416.
- Hastie, T., Tibshirani, R., & Friedman, J. (2009). The elements of statistical learning: data mining, inference, and prediction. Springer Science & Business Media. p. 66.
Images: