LoRA
- Hu, E. J., Shen, Y., Wallis, P., Allen-Zhu, Z., Li, Y., Wang, S., … & Chen, W. (2021). Lora: Low-rank adaptation of large language models. arXiv preprint arXiv:2106.09685.
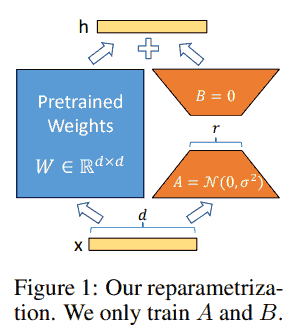
众所周知了, 略 (可以参考 这里).
We hypothesize that the change in weights during model adaptation also has a low “intrinsic rank”.
We limit our study to only adapting the attention weights for downstream tasks and freeze the MLP modules
QLoRA paper: “We find that the most critical LoRA hyperparameter is how many LoRA adapters are used in total and that LoRA on all linear transformer block layers is required to match full finetuning performance.”
初始化时 A 或 B 其中一个为零保证加了 AB 之后一开始的输出和原输出相同, 另一个非零保证优化过程中梯度不会恒为零.
注意 LoRA 并不省计算量, 只是大幅度节省了优化器需要存的参数, 可参考 这里 和 这里.
GaLore
- Zhao, J., Zhang, Z., Chen, B., Wang, Z., Anandkumar, A., & Tian, Y. (2024). Galore: Memory-efficient llm training by gradient low-rank projection. arXiv preprint arXiv:2403.03507.
Gradient Low-Rank Projection (GaLore), a training strategy that allows full-parameter learning but is more memory efficient than common low-rank adaptation methods such as LoRA.
Our key idea is to leverage the slow changing low-rank structure of the gradient of the weight matrix, rather than trying to approximate the weight matrix itself as low rank.
微调和预训练都可以用. 问题是全量微调的话多个任务不方便部署吧.
for weight in model.parameters():
grad = weight.grad
# original space -> compact space
lor_grad = project(grad)
# update by Adam, Adafactor, etc.
lor_update = update(lor_grad)
# compact space -> original space
update = project_back(lor_update)
weight.data += update
At time step $t$, $G_t \in \mathbb R^{m\times n}$ is the negative gradient matrix of weight $W_t$. The regular update is
\[W_T = W_0 + \eta \sum_{t=0}^{T-1}\tilde G_t = W_0 + \eta \sum_{t=0}^{T-1}\rho_t(G_t),\]where $eta$ is the learning rate, and $\rho_t$ is an entry-wise stateful gradient regularizer (e.g., Adam).
In GaLore, the $\tilde G_t$ in update becomes
\[\tilde G_t = P_t \rho_t(P_t'G_tQ_t)Q_t',\]where $P_t \in \mathbb R^{m\times r}$ and $Q_t \in \mathbb R^{n\times r}$. They are derived from SVD:
\[\begin{align*} G_t &= USV' \approx \sum_{i=1}^r s_i u_i v_i', \\ P_t &= (u_1, \dots, u_r) , \quad Q_t = (v_1, \dots, v_r). \end{align*}\]另外可参考
LoRA+
- Hayou, S., Ghosh, N., & Yu, B. (2024). LoRA+: Efficient Low Rank Adaptation of Large Models. arXiv preprint arXiv:2402.12354.
- 苏剑林. (Feb. 27, 2024). 《配置不同的学习率,LoRA还能再涨一点? 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/10001
LoRA 中 B 的学习率应该大于 A.
简单易用.
DoRA
- Liu, S. Y., Wang, C. Y., Yin, H., Molchanov, P., Wang, Y. C. F., Cheng, K. T., & Chen, M. H. (2024). DoRA: Weight-Decomposed Low-Rank Adaptation. arXiv preprint arXiv:2402.09353.
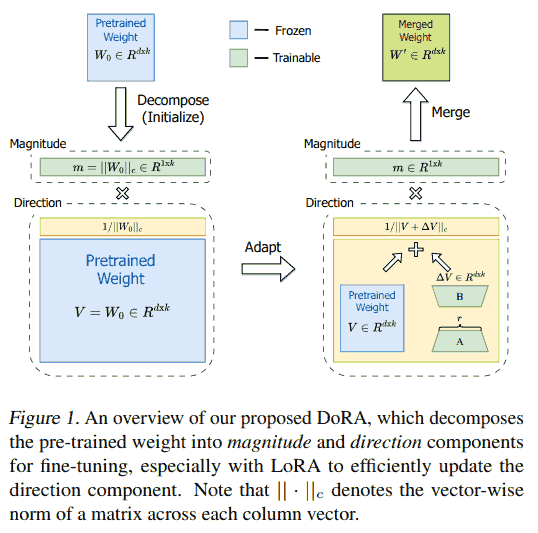
Our intuitions are two-fold. Firstly, we believe that limiting LoRA to concentrate exclusively on directional adaptation while also allowing the magnitude component to be tunable simplifies the task compared to the original approach, decomposition where LoRA is required to learn adjustments in both magnitude and direction. Secondly, the process of optimizing directional updates is made more stable through weight decomposition, which we delve into more thoroughly in Section.4.2.
第一点感觉没什么道理, 第二点还没仔细看过.
其他还有些很无聊的变种, 就略了.