Zhu, H., Zhang, C., Huang, J., Wu, J., & Xu, K. (2023). HiTIN: Hierarchy-aware Tree Isomorphism Network for Hierarchical Text Classification. arXiv preprint arXiv:2305.15182.
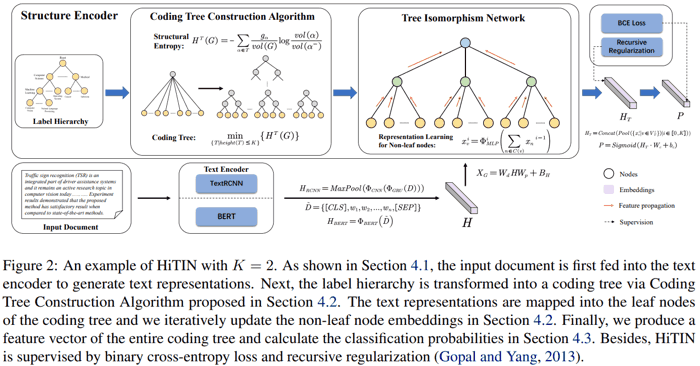
- (左上两个图) 先把原始的类别层级树结构转换成新的树结构 coding tree (作者自创概念).
- 获得文本表示之后 (上图右下 $H$), 转换成 coding tree 叶结点的 embedding (上图 $X_G$, 维度为 (叶结点数, 叶结点 embedding size)).
- (第一行第三个图) 然后用常规的 GNN, 在 coding tree 上, 从底向上, 递归地根据子结点的 embedding 获得结点的 embedding (子结点 embedding 先求和再 MLP). 最后把每一层的结点 embedding 做 pooling (上图右上 $H_T$), 拼接起来, 经过线性层得到最终 logits (标准的多标签分类).
主要创新点是上述第一步. 论文结果中, 相比其他针对层次分类的网络, 本网络参数少而且效果好很多.
重写的代码见 这里.
Coding tree
建议先看原论文附录. 原论文没图, 讲得也有点费解, 下面我随便画个图.
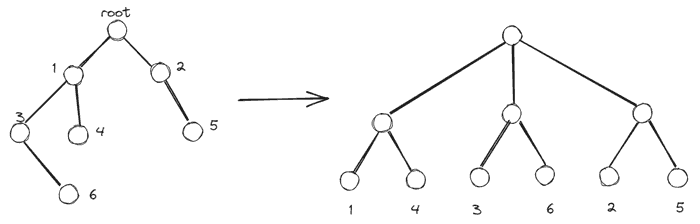
左边是原始层级结构, 有 6 个结点 (不考虑根结点). 转换成 coding tree 之后, coding tree 最底下一层包括了原始树的所有 6 个结点. Coding tree 的非叶结点可以看成原始树结点全体的不同级别的 partition (不交并集, 且并集为全集), 比如倒数第二层把原始 6 个结点分成了三块.
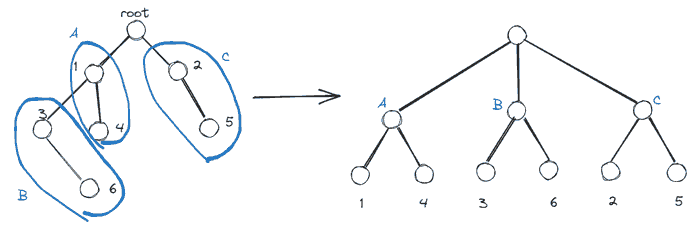
Coding tree 目标是使得在给定的 coding tree 深度下, structural entropy (作者提的概念) 最小的满足一定结构的树 (新叶结点是原树所有结点, 新非叶结点是原树所有结点的 partition). 作者设计了启发式算法 CodIng tRee Construction Algorithm (CIRCA), 将原始树转换成 coding tree. 这个算法的直观写在了论文附录中 (本文从略).
他的想法是通过引入一种熵, 以其为指导, 构建新树结构简化原始的层级结构 (论文中三个数据集 coding tree 最优深度都是 2, 也就是上图中的 3 层).
其他通用 tricks
Recursive regularization. 在层级分类中, 有亲子关系的类别应该更容易一起分类出来.
\[\sum_{n \in \mathcal N} \Vert w_n - w_{\pi(n)} \Vert^2,\]其中 $\mathcal N$ 是所有类别 (结点), $\pi(n)$ 表示结点 $n$ 的父结点, $w_n$ 表示最后全连接层权重 $W$ 中结点 $n$ 对应的向量.
おまけ
更多类似的可以参考 如何向深度学习模型中加入先验知识?