同事看表格检测的文章
- Tensmeyer, C., Morariu, V. I., Price, B., Cohen, S., & Martinez, T. (2019, September). Deep splitting and merging for table structure decomposition. In 2019 International Conference on Document Analysis and Recognition (ICDAR) (pp. 114-121). IEEE.
中的 Split Model 的 Inference 那节. 文章采用的表格检测分为两步, 先划若干条竖直线和水平线将图像分割为许多单元格, 再合并单元格得到表格.

第一步输入 $H \times W$ 的图像, 输出 $H \times 1$ 和 $W \times 1$ 的向量, 分别指示划水平线和竖直线的位置. 输出向量的每个元素介于 0~1, 表示划线的概率. 若直接根据概率阈值判断, 比如大于 0.5 则转换为 1, 否则转换为 0; 连续的 1 可以视为很粗的线, 连续的 0 则组成了单元格. 这样预测出来的两条线可能非常靠近, 导致中间的单元格很小, 显然不对. 文章采用的方法是把输出的概率值向量由 graphcut segmentation 转换为 0-1 序列.
Minimum cut
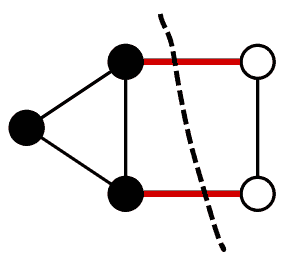
上述 graphcut segmentation 是求某个图的 minimum cut. 图的 cut 把图的结点分成两个不相交的子集. 如上图虚线把 5 个结点分成黑白两个不相交的子集. Min cut 是令某个指标最小化的 cut. 一个 cut 可以由 cut-set 刻画, 它是一个集合, 元素是符合下述条件的所有的边: 两端不同在一个结点子集里 (即一端黑一端白, 如上图红线).
下面考虑无向带权图, 考虑 min-cut 最小化 cut-set 中所有边的权重之和.
更一般的概念可参考 wiki, Cut (graph theory), Minimum cut, Max-flow min-cut theorem (这里有提到 Image segmentation problem). 概念很少, wiki 上讲得也很清楚.
文中的构造
代码见 TF_SPLERGE/model/graph_cut.py#L4-L25.
import networkx as nx
# 有改动
def graph_cut(probs, weight=0.75):
source = 's'
target = 't'
G = nx.Graph()
G.add_nodes_from([source, target])
G.add_nodes_from(i for i in range(len(probs)))
weighted_edges = []
for i, prob in enumerate(probs):
if i < len(probs) - 1:
weighted_edges.append((i, i + 1, weight))
weighted_edges.append((i, source, prob))
weighted_edges.append((i, target, 1 - prob))
G.add_weighted_edges_from(weighted_edges, weight='weight')
_, (source_set, _) = nx.minimum_cut(G, source, target, capacity='weight')
# 1 for nodes in source set, 0 for those in target set
res_row = [0] * len(probs)
for node in source_set:
if node != source:
res_row[node] = 1
return res_row
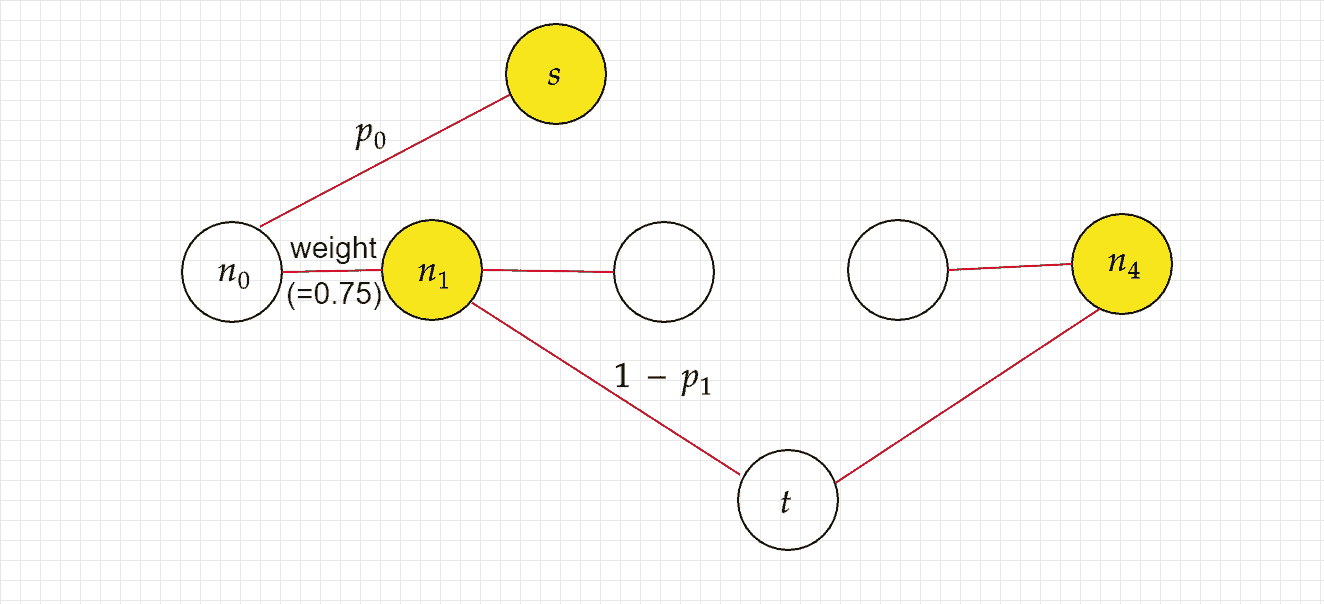
构造图. 假设 probs 有 5 个元素, $p_0$, $\dots$, $p_4$. 构造无向带全图如上 (懒得画出所有边了): 将 5 个结点 $n_0$, $\dots$, $n_4$ 排成一排, 相邻结点之间有边相连 (共 4 条边), 权重均为 weight (=0.75); 再引入额外的两个结点 $s$ 和 $t$ 与每个 $n_i$ 都有边 (共 10 条边), 其中 $s$ 和 $n_i$ 的边的权重为 $p_i$, $t$ 和 $n_i$ 权重 $1 - p_i$.
Cut. 考虑 $s-t$ cut, 即 $s$ 和 $t$ 处于不同的结点子集. 假设现在有个 cut 把结点分为黄白两个子集, 那么 cut-set 中所有边为上图中的红线, 下面把它们的权重之和称为 penalty.
输出 0-1 序列. 与 $s$ 处于相同结点子集的结点为 1, 其他为 0. 上图输出 0, 1, 0, 0, 1.
超参数 weight 的影响. 考虑极端情况 weight = 0, 显然当 $p_i < 0.5$ 时, 为了最小化 penalty, 我们希望将 $(n_i, s)$ 这条边的权重计入 penalty, 因此把 $n_i$ 划分给和 $t$ 相同的结点子集中. 导致那一排结点之间会更倾向出现黄白相间的情况, 因为它们之间的边权重为 0, 不影响 penalty.
越大的 weight 会使得那一排结点黄白相间的情况少. 使得图像分割粒度更粗, 能避免两条分割线靠得太近的情况.