主论文
- Ke, G., Meng, Q., Finley, T., Wang, T., Chen, W., Ma, W., … & Liu, T. Y. (2017). Lightgbm: A highly efficient gradient boosting decision tree. Advances in neural information processing systems, 30, 3146-3154.
LGB 的 light 指它比之前的 GBDT 实现 (比如 XGB) 更快. 核心是加速 GBDT 最耗时的求特征分裂点的部分 (时间复杂度 $O(\#\text{samples}\times\#\text{features})$ 或 histogram-based 的 $O(\#\text{bins}\times\#\text{features})$), 提出 Gradient-based One-Side Sampling (GOSS) 和 Exclusive Feature Bundling (EFB). 其中前者减少需要考虑的样本数 (主要考虑梯度大的样本), 后者压缩特征数, 从而实现加速. 结果除了速度, 精度也往往有提升.
Core ideas
Gradient-based one-side sampling 核心想法是梯度大的样本比较重要, 但如果直接不计算梯度小的样本会改变样本分布, 于是提出了 GOSS. 对梯度降序排序后, 保留前 $a\times 100\%$ 的样本, 从剩下的样本中随机抽取 $b\times 100\%$ 的样本, 并对后者的梯度乘 $(1-a) / b$ 以弥补, 以图减少样本分布的改变. 作者证明在大多情况下, 这种做法比完全随机采样好.
Exclusive feature bundling 核心想法是把不会同时取到非零值的特征组合当成一个特征, 从而减少特征数. In a sparse feature space, many features are mutually exclusive, i.e., they never take nonzero values simultaneously. 极端例子 one-hot encoding 本质上是一个特征.
More on EFB
论文简单说明了 EFB 是 NP-hard 问题, 所以需要近似求解.
We notice that there are usually quite a few features, although not 100% mutually exclusive, also rarely take nonzero values simultaneously. If our algorithm can allow a small fraction of conflicts, we can get an even smaller number of feature bundles and further improve the computational efficiency.
于是提出算法 3 把特征打包成 bundles. 时间复杂度是特征数的平方, 在整个训练过程中只做一次. 虽然如此, 对特征很多的情况, 为了进一步加速, 把算法中根据特征冲突数排序 (sortByDegree) 改为根据非零值数量排序.
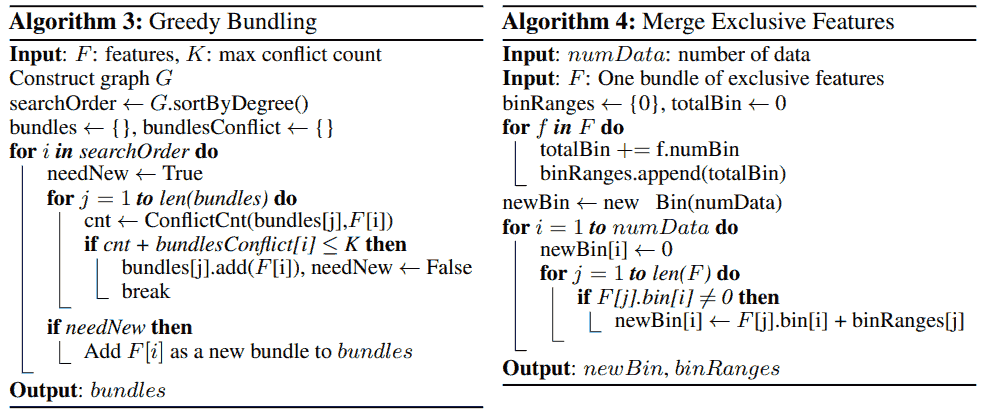
算法 4 合并 bundles 进一步减少特征数. 原文举的例子是一个特征取值为 $[0, 10)$, 另一个 $[0, 20)$, 把后一个特征加上 10, 组合成 $[0, 30)$ 的一个新特征 (bundle) 代替原先两个特征 (构造了原始特征和变化后 bundles 的一一对应).
Considerations on implementation
Leaf-wise (best-first) tree growth 原文 5.1 Overall Comparison 里一句带过.
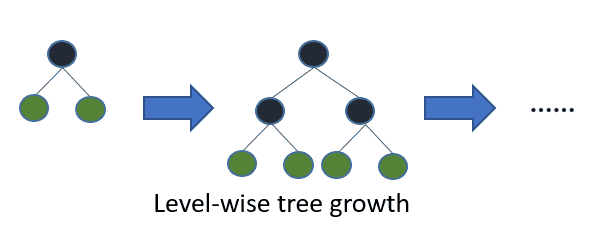
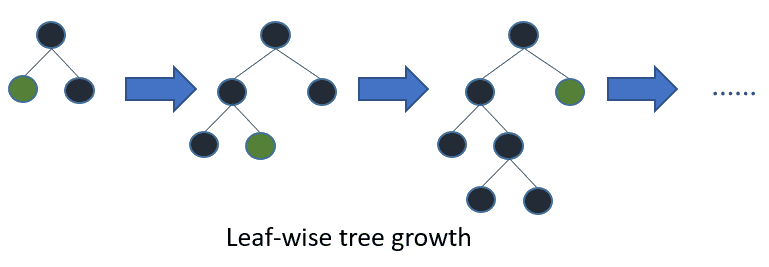
另外还有 optimal split for categorical features, 以及分布式, GPU 加速, 计算上的小 tricks 等, 这些在原论文没有提到, 参考 官方文档 和 作者的回答.
Further discussions: tree-based models vs neural networks
- 震灵. (2021, Sep 25). 神经网络能否代替决策树算法?. 知乎.
CatBoost 及其他 boost 变种很少用, 从略.