找中位数最暴力的方法是先排序再取中位数, 时间复杂度 $O(n\log n)$. 后来才得知中位数有时间复杂度 $O(n)$ 的算法, 事实上任意顺序统计量都可以用 $O(n)$ 时间找出.
In Expected Linear Time
考虑的问题是数组中取第 $k$ 小的数, 方便起见设 $k$ 从 0 开始计数.
主要想法来自快排. 先随机取一个 pivot 进行 partition, 即根据这个 pivot 将数组分为小于等于 pivot (左) 和大于 pivot (右) 两段.
- 如果 pivot 的位置恰好是 $k$, 那么就做完了.
- 如果左边长度大于 $k$, 说明要在左边找, 递归地调用快排, 否则就在右边找.
import random
def quickselect(nums, k):
'''
:param nums List[numeric]: 0-indexed
:param k int: 0-indexed
:return numeric: the k-th smallest number of nums
'''
pivot = random.randint(0, len(nums)-1)
nums[pivot], nums[-1] = nums[-1], nums[pivot]
i = -1
for j in range(len(nums)-1):
if nums[j] <= nums[-1]:
i += 1
nums[i], nums[j] = nums[j], nums[i]
i += 1
nums[i], nums[-1] = nums[-1], nums[i]
if i < k:
return quickselect(nums[i+1:], k-i-1)
elif i > k:
return quickselect(nums[:i], k)
else:
return nums[i]
记数组长度为 $n$, 算法时间复杂度为 $T(n)$, 以及 $Y$ 为进行 partition 后右子列的元素个数 (时间 $O(n)$), 则
\[\begin{align*} \mathbb E T(n) &\le \mathbb E\left[T\left(\max(Y-1,n-Y)\right) + O(n)\right]\\ & = \sum_{k=1}^n \frac1n\mathbb E\left[ T\left(\max(k-1,n-k)\right) \right] + O(n)\\ & \le \frac2n\sum_{k=[n/2]}^{n-1}\mathbb ET(k) + O(n). \end{align*}\]之后易证 (由 substitution method) $\mathbb ET(n) = O(n)$. 不过 worst-case 是 $O(n^2)$.
另外可以参考 Optimal algorithm for returning top k values from an array of length N. 简单地说是建小根堆, pop k 次, worst case $n + (k-1)\log n$ 次比较, 在这个基础上再稍微加点优化.mod
In Worst-Case Linear Time
不妨约定, 当偶数个元素时, 中位数取中间两个数中较小的那个.
算法记为 select 算法, 总体和前一个算法一样, 关键是找到一个好的 pivot. 记时间复杂度为 $T(n)$.
- 把数列分成 $\lceil n/5\rceil$ 组, 每组 5 个, 最后一组可能不足 5 个. 用时 $O(n)$.
- 找到每组 5 个元素的中位数. 用时 $O(n)$.
- 递归地调用
select找到 $\lceil n/5\rceil$ 个中位数的中位数 $x$. 用时 $T(\lceil n/5\rceil)$. - 根据 $x$ 进行 partition, 下略.
def median(nums):
return sorted(nums)[(len(nums)-1)//2]
def select(nums, k):
if len(nums) == 1:
return nums[0]
medians = [median(nums[i:i+5]) for i in range(0, len(nums), 5)]
pivot = select(medians, (len(medians)-1)//2)
i = -1
for j in range(len(nums)):
if nums[j] <= pivot:
i += 1
nums[i], nums[j] = nums[j], nums[i]
if i == k:
return pivot
elif i < k:
return select(nums[i+1:], k-i-1)
else:
return select(nums[:i+1], k)
考虑比 $x$ 大的元素个数, 有一半的组, 每组 3 个元素比 $x$ 大 (除了 $x$ 所在的组和最后一个不满 5 个元素的组以外). 故比 $x$ 大的元素个数至少有
\[3\left( \left\lceil \frac12 \left\lceil\frac{n}{5}\right\rceil \right\rceil -2 \right) \ge \frac{3n}{10} - 6.\]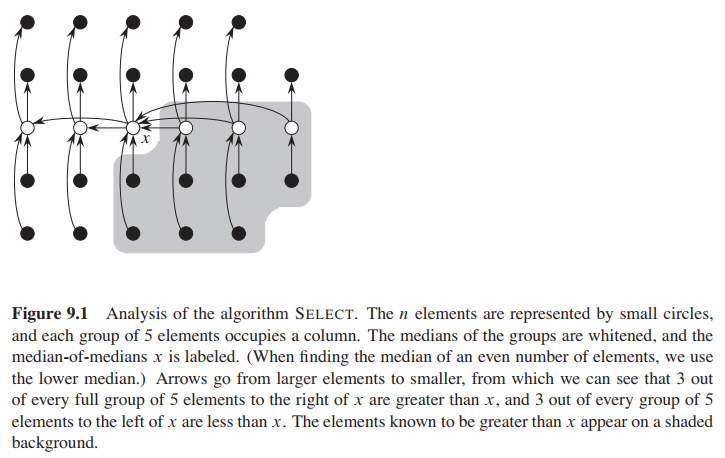
故最后递归用时 $T(7n/10 + 6)$. 因此
\[T(n) \le T(\lceil n/5\rceil) + T(7n/10 + 6) + O(n).\]易证 $T(n) = O(n)$.
注意到若分为每组 3 个, 则不能如上证明 $T(n) = O(n)$.
参考
Leiserson, C. E., Rivest, R. L., Cormen, T. H., & Stein, C. (2009). Introduction to algorithms (3rd ed.). Cambridge, MA: MIT press. pp. 215-222.
LeetCode 4
虽然和上面无关, 但是想法比较有意思.
Median of Two Sorted Arrays, 官方有个解答但是讲得太繁琐了.
假设数组分别为 $A=[a_0, \dots, a_{m-1}]$, $B = [b_0, \dots, b_{n-1}]$, 它们都已经排好序, 不妨假设 $m\le n$.
主要想法是把数组分为两段, $A$ 分为长度为 $i$ 和 $m-i$ 的两段, $B$ 分为长度为 $j$ 和 $n-j$ 的两段, 满足两个条件
- 前两段 (长度为 $i$ 和 $j$) 的任意元素小于后两段的任意元素.
- 前两段元素数量与后两段元素数量相等或者多一个 (根据总长度 $m+n$ 的奇偶性决定).
把数组如上分段之后就可以立即得到中位数. 下面要做的是寻找分段点. 由于条件 2, 我们在一个数组中找到分段点后, 另一个数组的分段点是唯一确定的, 于是方便起见从较短的数组 $A$ 找分段点, 用二分搜索即可.
关于具体的实现, 由条件 2,
\[(i + j) - (m-i + n-j) \in\{0, 1\},\]由此 $i + j = (m+n+1)//2$. 若在 $[0, n]$ 搜索 $j$, 那么由此得到的 $\hat i$ 可能为负, 所以在 $[0, m]$ 搜索 $i$ 更方便.
class Solution:
def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
m, n = len(nums1), len(nums2)
if m > n:
m, n = n, m
nums1, nums2 = nums2, nums1
if not n:
return None
left, right = 0, m
half = (m+n+1) // 2
while left <= right:
mid = (left+right) // 2
j = half - mid
if mid > 0 and nums1[mid-1] > nums2[j]:
# remark 1
right = mid - 1
elif mid < m and nums2[j-1] > nums1[mid]:
# remark 2
left = mid + 1
else:
if mid == 0:
max_left = nums2[j-1]
elif j == 0:
max_left = nums1[mid-1]
else:
max_left = max(nums1[mid-1], nums2[j-1])
if (m+n) % 2:
return max_left
if mid == m:
min_right = nums2[j]
elif j == n:
min_right = nums1[mid]
else:
min_right = min(nums2[j], nums1[mid])
return (max_left + min_right) / 2
Remark 1: 若 $\hat i > 0$, 则 $\hat j = (m+n+1)//2 - \hat i < (2n+1)//2 = n$.
Remark 2: 若 $\hat i < m$, 则 $\hat j = (m+n+1)//2 - \hat i > 2m / 2 -m = 0$.